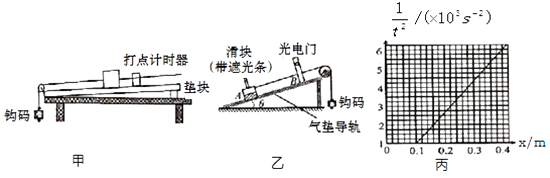
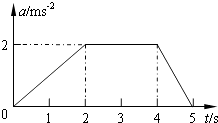
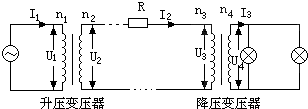
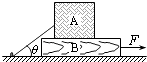
题目内容
【题目】如图甲,单匝圆形线圈c与电路连接,电阻R2两端与平行光滑金属直导轨p1e1f1、p2e2f2连接.垂直于导轨平面向下、向上有矩形匀强磁场区域Ⅰ、Ⅱ,它们的边界为e1e2 , 区域Ⅰ中垂直导轨并紧靠e1e2平放一导体棒ab.两直导轨分别与同一竖直平面内的圆形光滑绝缘导轨o1、o2相切连接,o1、o2在切点f1、f2处开有小口可让ab进入,ab进入后小口立即闭合.
已知:o1、o2的直径和直导轨间距均为d,c的直径为2d;电阻R1、R2的阻值均为R,其余电阻不计;直导轨足够长且其平面与水平面夹角为60°,区域Ⅰ的磁感强度为B0 . 重力加速度为g.在c中边长为d的正方形区域内存在垂直线圈平面向外的匀强磁场,磁感强度B随时间t变化如图乙所示,ab在t=0~ ![]() 内保持静止.
内保持静止.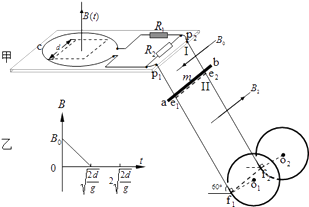
(1)求ab静止时通过它的电流大小和方向;
(2)求ab的质量m;
(3)设ab进入圆轨道后能达到离f1f2的最大高度为h,要使ab不脱离圆形轨道运动,求区域Ⅱ的磁感强度B2的取值范围并讨论h与B2的关系式.
【答案】
(1)
解:由法拉第电磁感应定律得c内感生电动势 E=S ![]() =d2
=d2 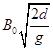 ①
①
由全电路欧姆定律有 E=IR ②(R2被ab短路)
联立①②解得:I= ![]()
![]() =
= ![]()
![]() ③
③
根据楞次定律和右手螺旋定则(或者平衡条件和左手定则)判断知ab中电流方向为a→b ④
(2)
解:由题意可知导轨平面与水平面夹角为 θ=60°,
对在t=0~ ![]() 内静止的ab受力分析有 mgsinθ=B0Id ⑤
内静止的ab受力分析有 mgsinθ=B0Id ⑤
联立③⑤解得:m= ![]()
![]() =
= ![]()
![]() ⑥
⑥
(3)
解:由题意知t= ![]() 后,c内的磁感强度减为零,ab滑入区域Ⅱ,
后,c内的磁感强度减为零,ab滑入区域Ⅱ,
由直导轨足够长可知ab进入圆形轨道时已达匀速直线运动,
设此时ab为v,其电动势为E2,电流为I2,
由平衡条件得 mgsinθ=B2I2d ⑦
由法拉第电磁感应定律得动生电动势 E2=B2dv ⑧
由全电路欧姆定律有 E2= ![]() ⑨(R1、R2并联)
⑨(R1、R2并联)
联立⑥⑦⑧⑨解得 v= ![]()
![]() =
= ![]()
![]() ⑩
⑩
由题意可知ab滑不过圆心等高点或者滑过圆轨道最高点均符合题意,分类讨论如下:
(ⅰ)当 ![]() mg
mg ![]() 即 B2≥
即 B2≥ ![]() 时,
时,
ab上滑过程由动能定理得 mgh= ![]() ,即h=
,即h= ![]()
(ⅱ) 设ab能滑到圆轨道最高点时速度为v1,根据牛顿第二定律应满足 mg≤ ![]()
所以当 ![]() ﹣mg
﹣mg ![]() (1+cosθ)≥
(1+cosθ)≥ ![]() 即B2≤
即B2≤ ![]() 时,
时,
ab能滑到圆轨道最高点,有 h= ![]() =
= ![]()
【解析】(1)ab静止时,由法拉第电磁感应定律求出c内感生电动势的大小,由欧姆定律求出电流的大小,由楞次定律判断电流的方向.(2)ab静止时受力平衡,重力沿导轨向下的分力与安培力二力平衡,由平衡条件列式可求ab的质量.(3)由题意知t= ![]() 后,c内的磁感强度减为零,ab滑入区域Ⅱ磁场,由于此段足够长,ab最终应做匀速直线运动,由平衡条件可求出其匀速运动的速度表达式.要使ab不脱离圆形轨道运动,有两种情况:ab滑不过圆心等高点或者滑过圆轨道最高,根据机械能守恒定律和圆周运动最高点的临界条件结合解答.
后,c内的磁感强度减为零,ab滑入区域Ⅱ磁场,由于此段足够长,ab最终应做匀速直线运动,由平衡条件可求出其匀速运动的速度表达式.要使ab不脱离圆形轨道运动,有两种情况:ab滑不过圆心等高点或者滑过圆轨道最高,根据机械能守恒定律和圆周运动最高点的临界条件结合解答.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案