题目内容
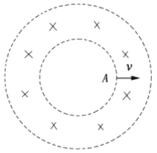
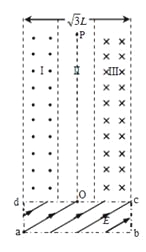
【题目】两个同轴(轴线水平)网状金属圆筒的截面如图所示,P的半径为![]() 、Q的半径为
、Q的半径为![]() ,在P圆筒内有沿轴线方向向外的匀强磁场,磁感应强度大小为
,在P圆筒内有沿轴线方向向外的匀强磁场,磁感应强度大小为![]() ,在P、Q两圆筒间加恒定电压U后,P、Q两圆筒之间有图示辐射状的电场,A、C是Q圆筒截面水平直径的端点,现将一电子从A点由静止释放,电子质量为m,电荷量为e,假设电子不会与P圆筒的金属网发生碰撞。求:
,在P、Q两圆筒间加恒定电压U后,P、Q两圆筒之间有图示辐射状的电场,A、C是Q圆筒截面水平直径的端点,现将一电子从A点由静止释放,电子质量为m,电荷量为e,假设电子不会与P圆筒的金属网发生碰撞。求:
(1)电子进入P圆筒时的速度大小;
(2)欲使电子在最短时间回到A点,电压U的大小;
(3)在电压U符合(2)问要求下,仍将电子从A点由静止释放,要求电子能够到达C点,并且在第一次到达C点之前,电子只能在AC直径及以下区域运动,需将P圆筒内磁场的磁感应强度大小变为![]() ,请你推导
,请你推导![]() 应满足的表达式。
应满足的表达式。

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]()
【解析】
(1)由动能定理得
![]()
解得:
v=![]()
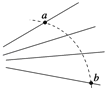
(2)欲使电子在最短时间内回到A点,电子应在磁场中发生三段相同弧长的圆周运动,如图1所示。如图2所示,r0表示在磁场中圆周运动的半径,
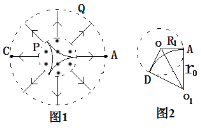
每段圆弧对应的圆心角为∠AO1D=60
tan30°=![]()
evB0 = ![]()
解得:
![]()
(3)电子能到达C点,需要电子在磁场中发生n段(n为整数且n≧2)相同弧长的圆周运动,设每段圆弧的半径为r1,对应的圆心角(弧度)为θ,则
θ=π-![]()
![]()
![]()
联立解得:
![]()

练习册系列答案
相关题目