题目内容
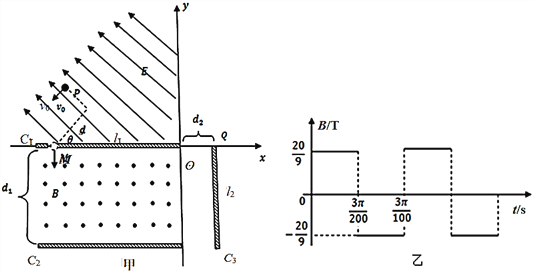
【题目】如图甲所示，在光滑绝缘水平桌面内建立xOy坐标系，在第Ⅱ象限内有平行于桌面的匀强电场，场强方向与x轴负方向的夹角θ=45°。在第Ⅲ象限垂直于桌面放置两块相互平行的平板C1、C2，两板间距为d1=0.6m，板间有竖直向上的匀强磁场，两板右端在y轴上，板C1与x轴重合，在其左端紧贴桌面有一小孔M，小孔M离坐标原点O的距离为l1=0.72m。在第Ⅳ象限垂直于x 轴放置一竖直平板C3，垂足为Q，Q、O相距d2=0.18m，板C3长l2=0.6m。现将一带负电的小球从桌面上的P点以初速度
垂直于电场方向射出，刚好垂直于x轴穿过C1板上的M孔，进入磁场区域。已知小球可视为质点，小球的比荷
，P点与小孔M在垂直于电场方向上的距离为
，不考虑空气阻力。求：
(1)匀强电场的场强大小；
(2)要使带电小球无碰撞地穿出磁场并打到平板C3上，求磁感应强度B的取值范围；
(3)以小球从M点进入磁场开始计时，磁场的磁感应强度随时间呈周期性变化，如图乙所示，则小球能否打在平板C3上？若能，求出所打位置到Q点距离；若不能，求出其轨迹与平板C3间的最短距离。 (
，计算结果保留两位小数)
【答案】(1) 
(2) 
(3) 
【解析】本题考查带电粒子在组合场中的运动，涉及有界磁场的临界问题。
（1）小球在第Ⅱ象限内做类平抛运动有：
由牛顿第二定律有： 
代入数据解得： 
（2）设小球通过M点时的速度为v，
由类平抛运动规律： 
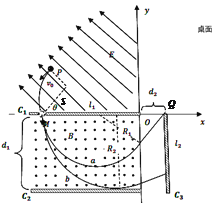
小球垂直磁场方向进入两板间做匀速圆周运动，轨迹如图
由牛顿第二定律有： 
得： 
小球刚好能打到Q点磁感应强度设为B1，此时小球的轨迹半径为R1
由几何关系有： 
解得： 
小球刚好不与C2板相碰时磁感应强度最小设为B2，此粒子的轨迹半径为R2
由几何关系有： 
解得： 
综合得磁感应强度的取值范围： 
（3）小球进入磁场做匀速圆周运动，设半径为R3，周期为T有：
由磁场周期
得小球在磁场中运动的轨迹如图
可得：一个磁场周期内小球在x轴方向的位移为3r
由分析知有： 
n=2
则小球能打在平板C3上，设位置到Q点距离为h有：
解得： 
m
