题目内容
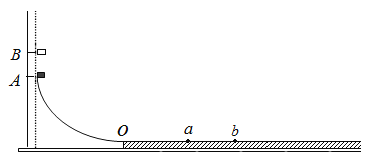
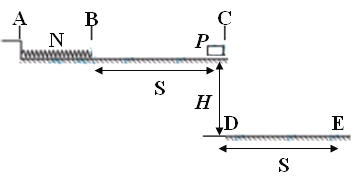
【题目】一可视为质点的质量为m的小铁块P,在一水平向左的推力作用下沿上面平台向左运动,与一端固定于A处的处于自然状态的轻质弹簧接触,触点为B,随后向左压缩弹簧,最深至N处时撤去推力,P向右回弹,飞离C处,刚好能击中下面平台的E处,若,AB段光滑,BC段长为S,BC段与铁块的动摩擦因数为μ,两平台高度差为H,DE长也为S,
求:(1)P在飞离C点的速度VC;
(2)弹簧被压缩到N时具有的弹性势能EP。
(3)若AB段与铁块的动摩擦因数也为μ,换一小铁块Q,从上面平台右边缘C处以水平初速度V0向左运动,与弹簧接触后,也最深压至N处,后向右弹回,刚好在C处静止。则Q的质量m’和NB的长度X各是多少?(此小问只需列出两个方程,不必求解)
【答案】(1)![]() (2)
(2)![]()
(3)两个方程:![]()
EP=μm′g(s+x)
【解析】
试题分析:1)小铁块P离开平台后做平抛运动,则有 ![]() ,s=vCt
,s=vCt
联立解得![]()
(2)根据能量守恒定律得: 弹簧被压缩到N时具有的弹性势能![]()
(3)对小铁块Q往返两个过程,分别运用能量守恒定律得:![]()
EP=μm′g(s+x)

练习册系列答案
相关题目