��Ŀ����
17�������۰˺š��롰�칬һ�š��Խӳɹ���ġ��칬-���ۡ������壬Ŀǰ��������̫�գ�ʵ�����й����˺��칤��һ���µĿ�Խ���칬-���ۡ������������Ϊm����������ΪM�����칬-���ۡ����������ĵľ���ΪR��������������ΪG�������й������Բ���������1�����칬-���ۡ��������ڹ�����ܵ����������������
��2�����칬-���ۡ��������������е�����T��
���� ��1������������������ʽ����������ܵ����������������
��2���������������ṩԲ���˶�������������е����ڣ�
��� �⣺��1���������������ɿɵ��������ܵ��������������Ϊ��
F=$G\frac{mM}{{R}^{2}}$
��2���������������ṩԲ���˶�������
$G\frac{mM}{{R}^{2}}=mR\frac{4{��}^{2}}{{T}^{2}}$
�ɵã����������е�����T=$\sqrt{\frac{4{��}^{2}{R}^{3}}{GM}}$
�𣺣�1�����칬-���ۡ��������ڹ�����ܵ��������������Ϊ$G\frac{mM}{{R}^{2}}$��
��2�����칬-���ۡ��������������е�����TΪ$\sqrt{\frac{4{��}^{2}{R}^{3}}{GM}}$��
���� ���������������ɣ�֪��������������������Բ���˶��������������������ṩ�����ɴ��ܸ��ݰ뾶��������Բ���˶���������Ĺ�ϵ��

��ϰ��ϵ�д�
�����Ŀ
6��һС��Ӿ�ֹ��ʼ���ȼ���ֱ���˶����ڵ�15s�ڵ�λ�Ʊȵ�14s�ڵ�λ�ƶ�0.2m��������˵����ȷ���ǣ�������
| A�� | С����ٶ�Ϊ0.1m/s2 | B�� | С���14s�ij��ٶ�Ϊ2.6m/s | ||
| C�� | С��ǰ15s�ڵ�ƽ���ٶ�Ϊ3.0m/s | D�� | С���15s�ڵ�λ��Ϊ2.9m |
2�� ��ͼ��ʾ������ˮƽ�����ϵ�ľ��B�ڣ�С��A��ϸ��Լ����������Բ���˶�ʱ��ϸ������ֱ����ļн�Ϊ�ȣ����ʱľ��������ĵ�����Ħ������С�ֱ�ΪFN1��f1�����ڽ�С������ϸ������ֱ����ļнǦ�ʱ�ͷţ���С��ڶ�����͵�ʱ��ľ��������ĵ�����Ħ������С�ֱ�ΪFN2��f2��ľ��ʼ�վ�ֹ���������¹�ϵ��ȷ���ǣ�������
��ͼ��ʾ������ˮƽ�����ϵ�ľ��B�ڣ�С��A��ϸ��Լ����������Բ���˶�ʱ��ϸ������ֱ����ļн�Ϊ�ȣ����ʱľ��������ĵ�����Ħ������С�ֱ�ΪFN1��f1�����ڽ�С������ϸ������ֱ����ļнǦ�ʱ�ͷţ���С��ڶ�����͵�ʱ��ľ��������ĵ�����Ħ������С�ֱ�ΪFN2��f2��ľ��ʼ�վ�ֹ���������¹�ϵ��ȷ���ǣ�������
 ��ͼ��ʾ������ˮƽ�����ϵ�ľ��B�ڣ�С��A��ϸ��Լ����������Բ���˶�ʱ��ϸ������ֱ����ļн�Ϊ�ȣ����ʱľ��������ĵ�����Ħ������С�ֱ�ΪFN1��f1�����ڽ�С������ϸ������ֱ����ļнǦ�ʱ�ͷţ���С��ڶ�����͵�ʱ��ľ��������ĵ�����Ħ������С�ֱ�ΪFN2��f2��ľ��ʼ�վ�ֹ���������¹�ϵ��ȷ���ǣ�������
��ͼ��ʾ������ˮƽ�����ϵ�ľ��B�ڣ�С��A��ϸ��Լ����������Բ���˶�ʱ��ϸ������ֱ����ļн�Ϊ�ȣ����ʱľ��������ĵ�����Ħ������С�ֱ�ΪFN1��f1�����ڽ�С������ϸ������ֱ����ļнǦ�ʱ�ͷţ���С��ڶ�����͵�ʱ��ľ��������ĵ�����Ħ������С�ֱ�ΪFN2��f2��ľ��ʼ�վ�ֹ���������¹�ϵ��ȷ���ǣ�������| A�� | FN1��FN2��f1��f2 | B�� | FN1��FN2��f1��f2 | C�� | FN1��FN2��f1��f2 | D�� | FN1��FN2��f1��f2 |
9�� ��ͼʾ�ĵ�·�У���Դ��ѹ���䣮�պϵ��K��L1��L2�����⣬-��ʱ������е�һյ��ͻȻ����������ѹ��Vl��ʾ����С����ѹ��V2��ʾ������������һ�����ԭ���ǣ�������
��ͼʾ�ĵ�·�У���Դ��ѹ���䣮�պϵ��K��L1��L2�����⣬-��ʱ������е�һյ��ͻȻ����������ѹ��Vl��ʾ����С����ѹ��V2��ʾ������������һ�����ԭ���ǣ�������
 ��ͼʾ�ĵ�·�У���Դ��ѹ���䣮�պϵ��K��L1��L2�����⣬-��ʱ������е�һյ��ͻȻ����������ѹ��Vl��ʾ����С����ѹ��V2��ʾ������������һ�����ԭ���ǣ�������
��ͼʾ�ĵ�·�У���Դ��ѹ���䣮�պϵ��K��L1��L2�����⣬-��ʱ������е�һյ��ͻȻ����������ѹ��Vl��ʾ����С����ѹ��V2��ʾ������������һ�����ԭ���ǣ�������| A�� | ��L1��· | B�� | ��Ll��· | C�� | ��L2��· | D�� | ��L2��· |
7�� ��ͼ��ʾ��һ������Ϊ-Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣮��һ������Ϊ+q������Ϊm�ĵ����ң���A���Գ��ٶ�v0�����ǵ���������˶�����B��ʱ�ٶ���С��Ϊv����֪��������ˮƽ��Ķ�Ħ������Ϊ�̡�AB�����ΪL0������������Ϊk��������
��ͼ��ʾ��һ������Ϊ-Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣮��һ������Ϊ+q������Ϊm�ĵ����ң���A���Գ��ٶ�v0�����ǵ���������˶�����B��ʱ�ٶ���С��Ϊv����֪��������ˮƽ��Ķ�Ħ������Ϊ�̡�AB�����ΪL0������������Ϊk��������
 ��ͼ��ʾ��һ������Ϊ-Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣮��һ������Ϊ+q������Ϊm�ĵ����ң���A���Գ��ٶ�v0�����ǵ���������˶�����B��ʱ�ٶ���С��Ϊv����֪��������ˮƽ��Ķ�Ħ������Ϊ�̡�AB�����ΪL0������������Ϊk��������
��ͼ��ʾ��һ������Ϊ-Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣮��һ������Ϊ+q������Ϊm�ĵ����ң���A���Գ��ٶ�v0�����ǵ���������˶�����B��ʱ�ٶ���С��Ϊv����֪��������ˮƽ��Ķ�Ħ������Ϊ�̡�AB�����ΪL0������������Ϊk��������| A�� | ������Խ��B�����������˶�������������� | |
| B�� | ��A��B�Ĺ����У��糡���Ե��������Ĺ�W=��mgL0+$\frac{1}{2}$mv02-$\frac{1}{2}$mv2 | |
| C�� | �ڵ��ɼ��γɵĵ糡�У�AB����Ʋ�UAB=$\frac{{��mg{L_0}+\frac{1}{2}m{v_0}^2-\frac{1}{2}m{v^2}}}{q}$ | |
| D�� | OB��ľ���Ϊ$\sqrt{\frac{kQq}{��mg}}$ |
 ��ͼ��һ�ʵ������������������ȼ���ֱ���˶����Ӿ���ԭ��O��ʼ��ʱ����ʱ�ٶ�Ϊ2m/s��������4��ʱ�䣬�ʵ�λ������Ϊ40m�����ʵ��˶��ļ��ٶȺ͵�5���ڵ�ƽ���ٶȴ�С��
��ͼ��һ�ʵ������������������ȼ���ֱ���˶����Ӿ���ԭ��O��ʼ��ʱ����ʱ�ٶ�Ϊ2m/s��������4��ʱ�䣬�ʵ�λ������Ϊ40m�����ʵ��˶��ļ��ٶȺ͵�5���ڵ�ƽ���ٶȴ�С��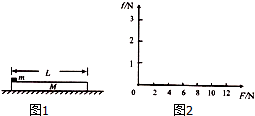 ��ͼ��ʾ������M=2kg��ľ�徲ֹ�ڹ⻬��ˮƽ�����ϣ���ľ�����˷���һ������m=1kg����С���Ժ��Ե����飬������ľ���Ķ�Ħ��������=0.2��ȡg=10m/s2������
��ͼ��ʾ������M=2kg��ľ�徲ֹ�ڹ⻬��ˮƽ�����ϣ���ľ�����˷���һ������m=1kg����С���Ժ��Ե����飬������ľ���Ķ�Ħ��������=0.2��ȡg=10m/s2������ ��ͼΪ������ֱ���˶�x-tͼ����
��ͼΪ������ֱ���˶�x-tͼ����