题目内容
2. 如图所示,放在水平地面上的木箱B内,小球A在细线约束下做匀速圆周运动时,细线与竖直方向的夹角为θ.设此时木箱与地面间的弹力和摩擦力大小分别为FN1和f1.现在将小球拉至细线与竖直方向的夹角θ时释放,当小球摆动到最低点时,木箱与地面间的弹力和摩擦力大小分别为FN2和f2.木箱始终静止不动,以下关系正确的是( )
如图所示,放在水平地面上的木箱B内,小球A在细线约束下做匀速圆周运动时,细线与竖直方向的夹角为θ.设此时木箱与地面间的弹力和摩擦力大小分别为FN1和f1.现在将小球拉至细线与竖直方向的夹角θ时释放,当小球摆动到最低点时,木箱与地面间的弹力和摩擦力大小分别为FN2和f2.木箱始终静止不动,以下关系正确的是( )| A. | FN1>FN2;f1>f2 | B. | FN1<FN2;f1>f2 | C. | FN1<FN2;f1<f2 | D. | FN1>FN2;f1<f2 |
分析 当小球A在细线约束下做匀速圆周运动时,由牛顿第二定律求出细线的拉力,再对木箱,根据平衡条件求出FN1和f1.
将小球拉至细线与竖直方向的夹角θ时释放,根据机械能守恒求出小球摆动到最低点时,由牛顿第二定律求出绳子的拉力,再对木箱,根据平衡条件求出FN2和f2.即可作出判断.
解答 解:设小球和木箱的质量分别为m和M.
当小球A在细线约束下做匀速圆周运动时,由牛顿第二定律可得:T1cosθ=mg,则细线的拉力 T1=$\frac{mg}{cosθ}$
对木箱,根据平衡条件可得:地面对木箱的支持力 FN1=T1cosθ+Mg=(m+M)g;
f1=T1sinθ=mgtanθ
将小球拉至细线与竖直方向的夹角θ时释放,根据机械能守恒得:
mgL(1-cosθ)=$\frac{1}{2}m{v}^{2}$
在最低点,由牛顿第二定律有:T2-mg=m$\frac{{v}^{2}}{L}$,解得 T2=mg(3-2cosθ),则FN2=T2+Mg=mg(3-2cosθ)+Mg
f2=0
故得:FN1<FN2;f1>f2.
故选:B
点评 解决本题的关键要分析受力,确定圆周运动的向心力来源,结合机械能守恒、平衡条件进行研究.

练习册系列答案
相关题目
10. 如图所示,水平放置的传送带足够长,它以恒定速率v顺时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.以下说法正确的是( )
如图所示,水平放置的传送带足够长,它以恒定速率v顺时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.以下说法正确的是( )
 如图所示,水平放置的传送带足够长,它以恒定速率v顺时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.以下说法正确的是( )
如图所示,水平放置的传送带足够长,它以恒定速率v顺时针运行,一小物体以水平向右的初速度v0滑上A端,物体与传送带间的动摩擦因数为μ.以下说法正确的是( )| A. | 如果v0=v,物体受到静摩擦力的作用 | |
| B. | 如果v0<v,物体受向右的滑动摩擦力作用直到匀速运动 | |
| C. | 如果v0>v,物体将先减速运动再匀速运动 | |
| D. | 如果v0<v,物体将先减速运动再匀速运动 |
14.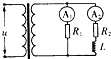 如图所示的电路中,A1、A2为相同的电流表,电阻R1、R2的阻值相同,线圈L的电阻不计,理想变压器原线圈接入u=Umsin2πft的交变电流后,电流表A1、A2的示数分别为I1、I2,则( )
如图所示的电路中,A1、A2为相同的电流表,电阻R1、R2的阻值相同,线圈L的电阻不计,理想变压器原线圈接入u=Umsin2πft的交变电流后,电流表A1、A2的示数分别为I1、I2,则( )
 如图所示的电路中,A1、A2为相同的电流表,电阻R1、R2的阻值相同,线圈L的电阻不计,理想变压器原线圈接入u=Umsin2πft的交变电流后,电流表A1、A2的示数分别为I1、I2,则( )
如图所示的电路中,A1、A2为相同的电流表,电阻R1、R2的阻值相同,线圈L的电阻不计,理想变压器原线圈接入u=Umsin2πft的交变电流后,电流表A1、A2的示数分别为I1、I2,则( )| A. | Um增大时,I1增大 | B. | Um增大时,I2减小 | C. | f增大时,I1增大 | D. | f增大时,I2减小 |
11. 一物体沿半径分别为r和R的半圆弧由A经B运动到C,经历的时间为t,如图所示,则它的平均速度和平均速率分别是( )
一物体沿半径分别为r和R的半圆弧由A经B运动到C,经历的时间为t,如图所示,则它的平均速度和平均速率分别是( )
 一物体沿半径分别为r和R的半圆弧由A经B运动到C,经历的时间为t,如图所示,则它的平均速度和平均速率分别是( )
一物体沿半径分别为r和R的半圆弧由A经B运动到C,经历的时间为t,如图所示,则它的平均速度和平均速率分别是( )| A. | $\frac{2(R+r)}{t}$;$\frac{π(R+r)}{t}$ | B. | $\frac{2(R+r)}{t}$,向东;$\frac{2(R+r)}{t}$ | ||
| C. | $\frac{2(R+r)}{t}$,向东;$\frac{π(R+r)}{t}$,向东 | D. | $\frac{2(R+r)}{t}$,向东;$\frac{π(R+r)}{t}$ |



