��Ŀ����
����Ŀ����ͼ��ʾ������Ǧ�=37��Ĺ⻬б���ϴ���һ��ֱб�����ϵ���ǿ�ų�����MNPQ���Ÿ�Ӧǿ��B�Ĵ�СΪ5T���ų�����d=0.55m����һ�߳�L=0.4m������m1=0.6kg������R=2���������ξ��ȵ����߿�abcdͨ��һ����ϸ�߿���⻬�Ķ�������һ����Ϊm2=0.4kg������������������ˮƽ���Ķ�Ħ��������=0.4�����߿��ͼʾλ���ɾ�ֹ�ͷţ����嵽�����ֵľ����㹻������ȡg=10m/s2 �� sin37��=0.6��cos37��=0.8����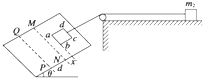
��1���߿�abcd��δ����ų����˶������У�ϸ���е�����Ϊ���٣�
��2����ab�߸ս���ų�ʱ���߿�ǡ��������ֱ���˶������߿���ͷ�ʱab�߾�ų�MN�߽�ľ���x���
��3���ڣ�2�����������£���cd��ǡ�뿪�ų��߽�PQʱ���ٶȴ�СΪ2m/s���������˶�������ab�߲���������Ϊ���٣�
���𰸡�
��1��
�⣺m1��m2�˶������У�������Ϊ�о�������ţ�ٵڶ����ɵã�
m1gsin �ȩ���m2g=��m1+m2��a��
�������ݽ�ã�a=2m/s2��
��m2Ϊ�о�������ţ�ٵڶ����ɵã�T����m2g=m2a��
�������ݽ�ã�T=2.4N
��2��
�⣺�߿����ų�ǡ��������ֱ���˶���������Ϊ�о�������ƽ�������ã�
m1gsin �ȩ���m2g�� ![]() =0��
=0��
�������ݽ�ã�v=1m/s��
ab��MNǰ�߿����ȼ����˶����У�v2=2ax��
�������ݽ�ã�x=0.25m
��3��
�⣺�߿�ӿ�ʼ�˶���cd��ǡ�뿪�ų��߽�PQʱ���������غ㶨�ɵã�
m1gsin �ȣ�x+d+L������m2g��x+d+L��= ![]() ��m1+m2��v12+Q��
��m1+m2��v12+Q��
�������ݽ�ã�Q=0.4J��
���ԣ�Qab= ![]() Q=0.1J
Q=0.1J
����������1���߿�abcd��δ����ų����˶������У��߿�������һ�������ٶȴ�С��ȵ��ȼ����˶����������巨����ţ�ٵڶ�����������ǵļ��ٶȴ�С����������Ϊ�о�������ʽ���ϸ����������2���߿����ų�ǡ���٣��������壬������Ϊ�㣬����ƽ�������Ͱ��������ٶȵĹ�ϵʽ����������˶����ٶȴ�С�������˶�ѧ��ʽ���x����3���߿�ӿ�ʼ�˶���cd��ǡ�뿪�ų�ʱ�����������غ㶨�����ab�߲���������Q��
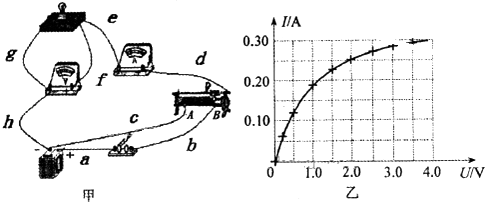
�����㾫�������ڱ��⿼��Ľ������ɣ���Ҫ�˽⽹������:Q=I2Rt��ʽ��Q��ʾ����ͨ�������������������λ��J.�������������ǶԴ������·���ǶԷǴ������·�������õIJ��ܵó���ȷ�𰸣�

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�