��Ŀ����
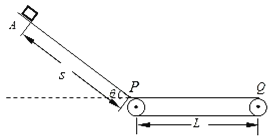
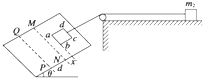
����Ŀ����ͼ��ʾ��ˮƽ���Ҷ˷�һ��С�ɺ��Ե�С��飬����m=0.1kg����v0=4m/s�����˶����˶����������d=1m��������ѹ������̣������ص�������ʱ�ٶȴ�Сv1=2m/s��ˮƽ����ˮƽ���ʹ��������ӣ����ʹ�����L=3m����v2=10m/s˳ʱ������ת�������ʹ��Ҷ���һ��ֱ���ڹ⻬Բ����������ӣ�Բ����뾶R=0.8m����������ʱ�����պ�װ�ý�Բ�����գ���g=10m/s2 �� sin53��=0.8��cos53��=0.6������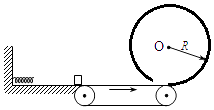
��1��������ˮƽ���Ķ�Ħ��������1��
��2�����ɾ��е����������Ep��
��3��Ҫʹ��������ֱԲ���������Բ��������ʹ��������Ķ�Ħ��������2Ӧ�����������
���𰸡�
��1��
�⣺С�����ˮƽ�������˶��ٷ��صĹ��̣����������غ㶨�ɵ�
��1mg2d= ![]() ��
�� ![]()
�������ݽ�� ��1=0.3
��2��
�⣺С���ӳ������˶�������ѹ������̵Ĺ��̣��������غ㶨�ɵ�
���ɾ��е���������� Ep= ![]() ����1mgd
����1mgd
�������ݽ�� Ep=0.5J
��3��
�⣺���������������ۣ�
���������Բ�����͵�ʱ�ٶ�Ϊv3ʱ��ǡ�õ���Բ���Ҳ�ȸߵ㣮
���ݻ�е���غ�� mgR= ![]() ���� v3=4m/s��v2=10m/s
���� v3=4m/s��v2=10m/s
˵������ڴ��ʹ���һֱ���ȼ����˶���
�ɶ��ܶ����ã���2mgL= ![]() ��
�� ![]()
��� ��2=0.2
���������Բ�����͵�ʱ�ٶ�Ϊv4ʱ��ǡ�õ���Բ�����ߵ㣮
��Բ�����ߵ��У�mg=m ![]()
��Բ�����͵㵽��ߵ�Ĺ��̣��ɻ�е���غ㶨�ɵ�
2mgR+ ![]() =
= ![]()
��� v4=2 ![]() m/s��v2=10m/s
m/s��v2=10m/s
˵������ڴ��ʹ���һֱ���ȼ����˶���
�ɶ��ܶ����ã���2mgL= ![]() ��
�� ![]()
��� ��2=0.6
����Ҫʹ��������ֱԲ���������Բ��������ʹ��������Ķ�Ħ��������2Ӧ����������Ǧ�2��0.2���2��0.6��
����������1��С�����ˮƽ�������˶��ٷ��صĹ��̣�����ת��Ϊ���ܣ����������غ㶨����������ˮƽ���Ķ�Ħ��������1����2���о�С���ӳ������˶�������ѹ������̵Ĺ��̣��������غ㶨���ɾ��е����������Ep����3����黬�ϴ��ʹ����ڻ���Ħ�����������¼��٣���Ħ��������2��ͬ�����پ��벻ͬ������Բ������ij��ٶȾͲ�ͬ�����ǡ�õ���Բ���Ҳ�ȸߵ㡢Բ���Ҳ�ȸߵ��Բ�����ߵ�ʱ�ٶȣ�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ���ܶ�����Ħ��������2�ķ�Χ��
�����㾫����������Ĺؼ��������ⵯ�����ܵ����֪ʶ�����յ����������������ڷ��������α�����е��������Լ��Թ��ܹ�ϵ�����⣬�˽ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1��