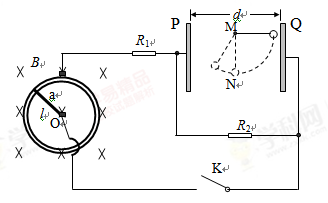
题目内容
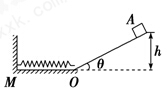
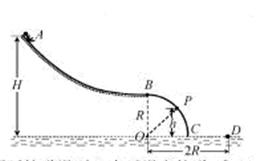
如图所示，粗糙的斜面AB下端与光滑的圆弧轨道BCD相切于B，整个装置竖直放置，C是最低点，圆心角θ=37°，D与圆心O等高，圆弧轨道半径R =1m，斜面长L=4m，现有一个质量m =0.1kg的小物体P从斜面AB上端A点无初速下滑，物体P与斜面AB之间的动摩擦因数为μ=0.25。不计空气阻力，g=10m/s2，sin37o=0.6，cos37o=0.8，求：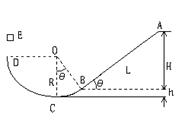
（1）物体P第一次通过C点时的速度大小
；
（2）物体P第一次通过C点时对轨道的压力
；
（3）物体P第一次离开D点后在空中做竖直上抛运动到最高点E，接着从空中又返回到圆轨道和斜面，在这样多次反复的整个运动过程中，物体P对C点处轨道的最小压力min。
（1）
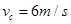（2）4.6N（3）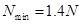
解析试题分析：（1）物体P从A下滑经B到C过程中根据动能定理：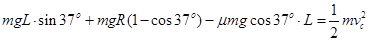
（3分）
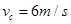解得（1分）
（2）物体在C点，根据牛顿第二定律得：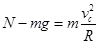
（2分）
解得N =4.6N （1分）
根据牛顿第三定律，物体P对C点的压力为4.6N （1分）
（3）物体P最后在B与其等高的圆弧轨道上来回运动时，经C点压力最小，
由B到C根据机械能守恒得：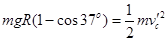
（2分）
解得 
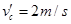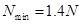， （2分）
考点：考查了牛顿第二定律，动能定理，机械能守恒的综合应用
练习册系列答案
阅读快车系列答案
相关题目
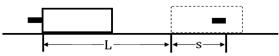
如右图所示，长为L的长木板水平放置，在木板的A端放置一个质量为m的小物块．现缓慢地抬高A端，使木板以左端为轴转动，当木板转到与水平面的夹角为α时小物块开始滑动，此时停止转动木板，小物块滑到底端的速度为v，则在整个过程中( )
| A．支持力对物块做功为0 |
B．支持力对小物块做功为 |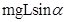
| C．摩擦力对小物块做功为 |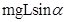
D．滑动摩擦力对小物块做功为 |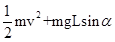
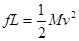
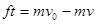
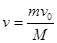
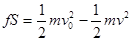
取
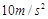。求：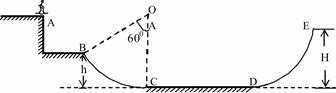
；
；
）
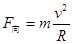