题目内容
如图所示,质量为M的木块放在光滑的水平面上,质量为m的子弹以速度v0沿水平面射中木块,并最终留在木块终于木块一起以速度v运动,已知当子弹相对木块静止时,木块前进距离L,子弹进入木块的深度为s,此过程经历的时间为t。若木块对子弹的阻力f视为恒定,则下列关系式中正确的是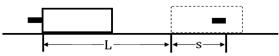
A.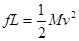 | B.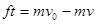 |
C.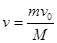 | D.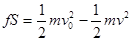 |
AB
解析试题分析:由动能定理,对M可得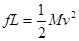 ,A选项正确;由动量定理,对m可列得
,A选项正确;由动量定理,对m可列得 ,选项B正确;对Mm整体 ,根据动量守恒
,选项B正确;对Mm整体 ,根据动量守恒 ,解得
,解得 ,选项C错误;根据能量守恒定律得
,选项C错误;根据能量守恒定律得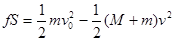 ,选项D错误。
,选项D错误。
. 考点:动能定理、动量定理、动量守恒定律及能量守恒定律。

如图所示,楔形木块abc固定在水平面上,粗糙斜面ab和光滑斜面bc与水平面的夹角相同,顶角b处安装一定滑轮。质量分别为M、m(M>m)的滑块,通过不可伸长的轻绳跨过定滑轮连接,轻绳与斜面平行。两滑块由静止释放后,沿斜面做匀加速运动。若不计滑轮的质量和摩擦,在两滑块沿斜面运动的过程中 ( )
| A.两滑块组成的系统机械能守恒 |
| B.重力对M做的功等于M动能的增加 |
| C.轻绳对m做的功等于m机械能的增加 |
| D.两滑块组成系统的机械能损失等于M克服摩擦力做的功 |
水平传送带匀速运动,速度大小为v,现将一小工件轻轻地放在传送带上,它将在传送带上滑动一段距离后,速度才达到v,而与传送带相对静止.设小工件的质量为m,它与传送带间的动摩擦因数为μ,在m与皮带相对运动的过程中( )
| A.工件是变加速运动 |
| B.滑动摩擦力对工件做功mv2/2 |
| C.工件相对传送带的位移大小为v2/(2µg) |
| D.工件与传送带因摩擦产生的内能为mv2/2 |
一个高尔夫球静止于平坦的地面上,在t=0时球被击出,飞行中球的速率与时间的关系如图所示.若不计空气阻力的影响,根据图象提供的信息可以求出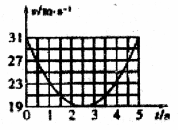
| A.高尔夫球在何时落地 |
| B.高尔夫球上升的最大高度 |
| C.人击球时对高尔夫球做的功 |
| D.高尔夫球落地时离击球点的距离 |
质量为m的物体,由静止开始下落,由于阻力作用,下落的加速度为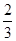 g,在物体下落h的过程中,下列说法中正确的是:( )
g,在物体下落h的过程中,下列说法中正确的是:( )
A.物体的动能增加了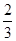 mgh mgh | B.物体的机械能减少了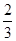 mgh mgh |
C.物体克服阻力所做的功为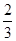 mgh mgh | D.物体的重力势能减少了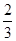 mgh mgh |
足够长的水平传送带始终以速度 匀速运动,某时刻,一质量为m、速度大小为
匀速运动,某时刻,一质量为m、速度大小为 ,方向与传送带运动方向相反的物体,在传送带上运动,最后物体与传送带相对静止。物体在传送带上相对滑动的过程中,滑动摩擦力对物体做的功为W1,传送带克服滑动摩擦力做的功W2,物体与传送带间摩擦产生的热量为Q,则( )
,方向与传送带运动方向相反的物体,在传送带上运动,最后物体与传送带相对静止。物体在传送带上相对滑动的过程中,滑动摩擦力对物体做的功为W1,传送带克服滑动摩擦力做的功W2,物体与传送带间摩擦产生的热量为Q,则( )
| A.W1=mv2 | B.W1=2m 2 2 | C.W2=m 2 2 | D.Q=2m 2 2 |
足够长的水平传送带始终以速度v匀速运动,某时刻使一质量为m,初速度大小也为v的物体,沿与传送带运动方向相反的方向在传送带上滑动.最后物体的速度与传送带相同.在物体相对传送带滑动的过程中,传送带克服摩擦力做的功为W,滑动摩擦力对物体的冲量为I,物体与传送带间摩擦生热为Q,则下列判断正确的是( )
| A.W=mv2/2 I=mv/2 Q=mv2 |
| B.W=0 I=mv Q=2mv2 |
| C.W=2mv2 I=2mv Q=2mv2 |
| D.W=2mv2 I=0 Q=0 |
 ;
; ;
;