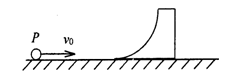
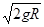题目内容
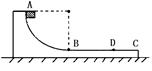
光滑水平面上有一质量为M滑块，滑块的左侧是一光滑的圆弧，圆弧半径为R="l.0" m。一质量为m的小球以速度v0。向右运动冲上滑块。已知M= 4m，g取l0m/s2，若小球刚好没跃出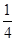
圆弧的上端，求：
①小球的初速度v0是多少?
②滑块获得的最大速度是多少?
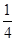圆弧的上端，求：①小球的初速度v0是多少?
②滑块获得的最大速度是多少?
（i）v0=5m/s （ii）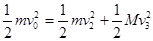
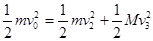
（i）当小球上升到滑块上端时，小球与滑块水平方向速度相同，设为v1，根据水平方向动量守恒有：
………………① （2分）
因系统机械能守恒，所以根据机械能守恒定律有：
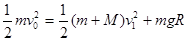……………………②
解得v0=5m/s ……………………③ （2分）
（ii）小球到达最高点以后又滑回，滑块又做加速运动，当小球离开滑块后滑块速度最大。研究小球开始冲上滑块一直到离开滑块的过程，根据动量守怦和动能守恒有：
……………………④ （2分）
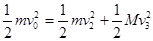………………⑤ （2分）
本题考查动量守恒定律和能量守恒定律的结合问题，当滑到最高点时，两物体速度相同，水平方向不受外力动量守恒和机械能守恒，列式求解
………………① （2分）因系统机械能守恒，所以根据机械能守恒定律有：
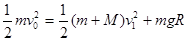……………………② 解得v0=5m/s ……………………③ （2分）
（ii）小球到达最高点以后又滑回，滑块又做加速运动，当小球离开滑块后滑块速度最大。研究小球开始冲上滑块一直到离开滑块的过程，根据动量守怦和动能守恒有：
……………………④ （2分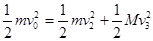） ………………⑤ （2分）本题考查动量守恒定律和能量守恒定律的结合问题，当滑到最高点时，两物体速度相同，水平方向不受外力动量守恒和机械能守恒，列式求解
练习册系列答案
备战中考寒假系列答案
相关题目
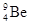)时，会产生一种看不见的、贯穿能力极强的不知名射线和另一种新粒子。经过研究发现，这种不知名射线具有如下的特点：① 在任意方向的磁场中均不发生偏转；② 这种射线的速度不到光速的十分之一；③ 用它轰击含有静止的氢核的物质，可以把氢核打出来。用它轰击含有静止的氮核的物质，可以把氮核打出来。并且被打出的氢核的最大速度vH和被打出的氮核的最大速度vN之比等于15 : 2。若该射线中的粒子均具有相同的能量，与氢核和氮核均发生正碰，且碰撞中没有机械能的损失。已知氢核的质量MH与氮核的质量MN之比等于1 : 14。 
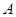位置有一个小球从静止开始下落，在
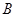位置接触弹簧的上端，在
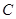位置小球所受弹力大小等于重力在
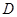位置小球速度减小到零，在小球的下降阶段中，以下说法正确的是( )
