题目内容
12. 如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板,两球静止,两细线与水平方向的夹角α=30°,弹簧水平,以下说法正确的是( )
如图所示,轻弹簧两端拴接两个质量均为m的小球a、b,拴接小球的细线固定在天花板,两球静止,两细线与水平方向的夹角α=30°,弹簧水平,以下说法正确的是( )| A. | 细线拉力大小为mg | B. | 弹簧的弹力大小为$\frac{\sqrt{3}}{2}$mg | ||
| C. | 剪断左侧细线瞬间,b球加速度为0 | D. | 剪断左侧细线瞬间,a球加速度为2g |
分析 根据共点力平衡求解细线的拉力和弹簧的弹力大小.剪断细线的瞬间,弹簧的弹力不变,结合牛顿第二定律求出a球的瞬时加速度.
解答 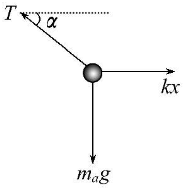 解:AB、对a球分析,
解:AB、对a球分析,
运用共点力平衡条件得:细线的拉力为:T=$\frac{mg}{sinα}$=2mg
弹簧的弹力为:F=mgcotαα=$\sqrt{3}$mg,故AB错误.
C、剪断左侧细线的瞬间,弹簧的弹力不变,故小球b所受的合力F合=0,加速度为0.故C正确.
D、剪断左侧细线的瞬间,弹簧的弹力不变,小球a所受的合力F合=T=2mg,根据牛顿第二定律得:a=2g,故D正确;
故选:CD.
点评 本题考查了牛顿第二定律和共点力平衡的基本运用,知道剪断细线的瞬间,弹簧的弹力不变.

练习册系列答案
相关题目
2.如图所示的直线和曲线分别是在平直公路上行驶的汽车a和b的位移-时间(x-t)图线.由图可知( )

| A. | 在0到t1这段时间内,a车的速度大于b车的速度 | |
| B. | 在0到t1这段时间内,a车的位移等于b车的位移 | |
| C. | 在t1到t2这段时间内,a车的平均速度大于b车的平均速度 | |
| D. | 在t1到t2这段时间内,a车的平均速度等于b车的平均速度 |
7.关于波的说法中,正确的是( )
| A. | 产生多普勒效应的原因是波源频率发生了变化 | |
| B. | 发生干涉现象时,介质中振动加强的点,振动能量最大,减弱点振动能量可能为零 | |
| C. | 振动图象和波的图象中,横坐标所反映的物理意义是不同的 | |
| D. | 超声波比次声波更容易发生衍射 | |
| E. | 在地球表面上走得很准的摆钟搬到月球表面上,其摆动周期变大 |
17.一个作初速度为零的匀加速直线运动的物体,已知它在第一个△t内通过的位移为s1,△t未知,则可求出( )
| A. | 第n个△t 内的位移 | B. | 物体运动的加速度 | ||
| C. | n△t 内物体的位移 | D. | 第一个△t 内的平均速度 |
4. 如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则( )
如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则( )
 如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则( )
如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则( )| A. | A测得两飞船间的距离大于L | |
| B. | B测得两飞船间的距离小于L | |
| C. | 当B向A发出一束光信号,A测得该信号的速度为c | |
| D. | 当B向A发出一束光信号,A测得该信号的速度为cv |

 某小型发电站发电机输出的交流电压为500V,输出的最大电功率为50kW,用电阻为3Ω的输电线向远处送电,要求输电线上损失功率为输电功率的0.6%,则发电站要安装一升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器)求:
某小型发电站发电机输出的交流电压为500V,输出的最大电功率为50kW,用电阻为3Ω的输电线向远处送电,要求输电线上损失功率为输电功率的0.6%,则发电站要安装一升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器)求: 在“验证力的平行四边形定则”的实验中某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
在“验证力的平行四边形定则”的实验中某同学的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.