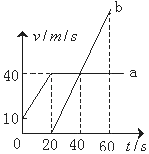��Ŀ����
����Ŀ����ͼ��ʾ��ˮƽ���õ������⻬ƽ�н�������a��b��cλ��ͬһˮƽ���ϣ��������Ϊd=1m������ac����һ����Ϊm=1kg�Ľ�����MN �� �����������촹ֱ����ʼ�սӴ����ã����ĵ���r=2��������ĵ�����Բ��ƣ��ڵ���bc���һ��ֵR=2���ĵ��ݣ�����ac���һ�����ѹ��������װ�÷��ڴŸ�Ӧǿ��B=2T����ǿ�ų��У��ų�����ֱ����ƽ�����£��ֶ�MNʩ��ˮƽ���ҵ�����F �� ʹ���Ӿ�ֹ��ʼ�˶��������ﵽ�ȶ�ʱ���ٶ�Ϊ1.5m/s����ˮƽ�������ʺ㶨����ˮƽ�����Ĺ���ΪW����ʱ��ѹ������ΪV��
���𰸡�3��5
���������ɷ����ڵ�Ÿ�Ӧ���ɣ����У�E=Bdv=2��1��1.5V=3V��
�����ĸ�Ӧ���� 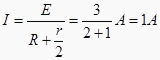
�������Ĵ�СFA=BId=2��1��1N=2N��
��ˮƽ�����Ĺ���P=Fv=FAv=2��1.5W=3W��
��ѹ����ʾ�� ![]() ��
��
���Դ��ǣ�3��5��
�����㾫����������Ŀ����֪������������ζ��ɵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ������ζ���������һ������ĸ�Ӧ����������ж��������ֶ���ֻ�����ڵ����и�Ÿ����˶��������������������ֶ����ж�������ζ����ж���㣮

��ϰ��ϵ�д�
�����Ŀ