��Ŀ����
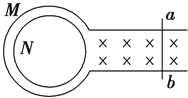
����Ŀ����ͼ�ף��̶��ڹ⻬ˮƽ���ϵ��������ν����߿�����n=20���ܵ���R=2.5�����߳�L=0.3m�����������뾶��Ϊ ![]() ��Բ����ǿ�ų������У��߿����Ҳ�Բ�����غϣ��߿�ױ��е������Բ�����غϣ��Ÿ�Ӧǿ��B1��ֱˮƽ�����⣬��С���䣻B2��ֱˮƽ�������С��ʱ��仯��B1��B2��ֵ��ͼ����ʾ����������
��Բ����ǿ�ų������У��߿����Ҳ�Բ�����غϣ��߿�ױ��е������Բ�����غϣ��Ÿ�Ӧǿ��B1��ֱˮƽ�����⣬��С���䣻B2��ֱˮƽ�������С��ʱ��仯��B1��B2��ֵ��ͼ����ʾ���������� 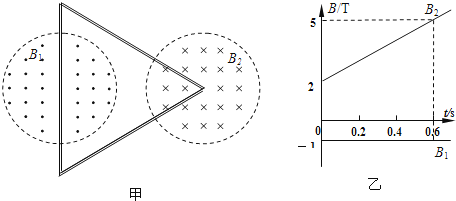
A.ͨ���߿��и�Ӧ��������Ϊ��ʱ�뷽��
B. t=0ʱ�̴����߿�Ĵ�ͨ��Ϊ0.1Wb
C.��t=0.6s��ͨ���߿��еĵ���Ϊ0.12C
D.����t=0.6s�߿��в���������Ϊ0.06J
���𰸡�A,C,D
�����������A���ɴŸ�Ӧǿ��B1��ֱˮƽ�����⣬��С���䣻B2��ֱˮƽ�������С��ʱ�������߿�Ĵ�ͨ����С������ζ��ɿɵã��߿��и�Ӧ��������Ϊ��ʱ�뷽��A��ȷ�� B��t=0ʱ�̴����߿�Ĵ�ͨ��Ϊ�� ![]() ���� B����
���� B����
C����t=0.6s��ͨ���߿��еĵ��� 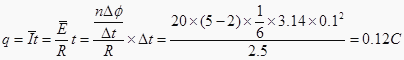 ����C��ȷ��
����C��ȷ��
D����  ����D��ȷ��
����D��ȷ��
��ѡ��ACD��
������������ζ����жϸ�Ӧ�����ķ����ݴ�ͨ����=BS��⣻�� ![]() �����������Q=I2Rt���������
�����������Q=I2Rt���������
�����㾫����������Ĺؼ�����������ζ��ɵ����֪ʶ��������ζ���������һ������ĸ�Ӧ����������ж��������ֶ���ֻ�����ڵ����и�Ÿ����˶��������������������ֶ����ж�������ζ����ж���㣮