题目内容
如图所示,光滑绝缘的正方形水平桌面边长为d=0.48m,离地高度h=1.25m.桌面上存在一水平向左的匀强电场(其余位置均无电场),电场强度E=1×104N/C.在水平桌面上某一位置P处有一质量m=0.01kg,电量q=1×10-6C的带正电小球以初速v0=1m/s向右运动.空气阻力忽略不计,重力加速度g=10m/s2
(1)求小球在桌面上运动时的加速度;
(2)P处距右端桌面多远时,小球从开始运动到最终落地的水平距离最大,并求出该最大水平距离.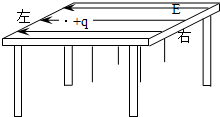
(1)求小球在桌面上运动时的加速度;
(2)P处距右端桌面多远时,小球从开始运动到最终落地的水平距离最大,并求出该最大水平距离.

(1)对小球受力分析,受到重力、支持力和电场力,重力和支持力平衡,根据牛顿第二定律,有
a=
=
=1.0m/s2 方向:水平向左
(2)球先向右减速,假设桌面足够长,减为零的过程,有
x=
=0.5m,大于桌面边长,故小球一直减速;
设球到桌面右边的距离为x1,球离开桌面后作平抛运动的水平距离为x2,则x总=x1+x2
由v2-v02=-2ax1
代入得 v=
=
设平抛运动的时间为t,根据平抛运动的分位移公式,有
h=
gt2
代入得t=0.5s
水平方向,有
x2=vt=0.5
故 x总=x1+0.5
令y=
则 x总=
故,当y=
即x1=
m时,水平距离最大
最大值为:xm=
m
即距桌面右端
m处放入,有最大水平距离为
m.
a=
| F |
| m |
| qE |
| m |
(2)球先向右减速,假设桌面足够长,减为零的过程,有
x=
| v2 |
| 2a |
设球到桌面右边的距离为x1,球离开桌面后作平抛运动的水平距离为x2,则x总=x1+x2
由v2-v02=-2ax1
代入得 v=
| 1-2×1×x1 |
| 1-2x1 |
设平抛运动的时间为t,根据平抛运动的分位移公式,有
h=
| 1 |
| 2 |
代入得t=0.5s
水平方向,有
x2=vt=0.5
| 1-2x1 |
故 x总=x1+0.5
| 1-2x1 |
令y=
| 1-2x1 |
| 1-y2+y |
| 2 |
故,当y=
| 1 |
| 2 |
| 3 |
| 8 |
最大值为:xm=
| 5 |
| 8 |
即距桌面右端
| 3 |
| 8 |
| 5 |
| 8 |

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
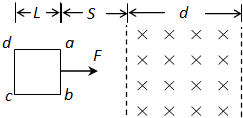 如图所示,光滑绝缘的水平面内有竖直方向的宽度为d的匀强磁场区,磁场的磁感应强度为B.正方形金属线框abcd边长为L(L<d),质量为m,现对线框施加垂直于ab边的水平恒力F使线框从磁场左侧距磁场S处由静止开始运动,如果ab边刚进入磁场时的速度为v0,cd边刚穿出磁场时的速度也为v0,则从ab边刚进入磁场到cd边刚穿出磁场的整个过程( )
如图所示,光滑绝缘的水平面内有竖直方向的宽度为d的匀强磁场区,磁场的磁感应强度为B.正方形金属线框abcd边长为L(L<d),质量为m,现对线框施加垂直于ab边的水平恒力F使线框从磁场左侧距磁场S处由静止开始运动,如果ab边刚进入磁场时的速度为v0,cd边刚穿出磁场时的速度也为v0,则从ab边刚进入磁场到cd边刚穿出磁场的整个过程( )| A、线框有一阶段在做匀加速运动 | B、线框ab边在刚进入磁场时可能做加速运动 | C、线框ab边在刚穿出磁场时一定是先做减速运动 | D、线框中产生的热量为F(d+S+L) |
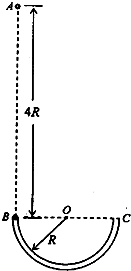 如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直平面内,管口B、C的连线是水平直径.现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R.从小球进入管口开始,整个空间突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点.设小球运动过程中带电量没有改变,重力加速度为g.求:
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直平面内,管口B、C的连线是水平直径.现有一带正电小球(可视为质点)从B点正上方的A点自由下落,A、B两点间距离为4R.从小球进入管口开始,整个空间突然加上一个匀强电场,电场力在竖直向上的分力大小与重力大小相等,结果小球从管口C处脱离圆管后,其运动轨迹最后经过A点.设小球运动过程中带电量没有改变,重力加速度为g.求: 如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内,管口B,C的连线水平.质量为m的带正电小球从B点正上方的A点自由下落A,B两点间距离为4R.从小球(小球直径小于细圆管直径)进人管口开始,整个空间中突然加上一个斜向左上方的匀强电场,小球所受电场力在竖直方向上的分力方向向上,大小与重力相等,结果小球从管口 C处离开圆管后,又能经过A点.设小球运动过程中电荷量没有改变,重力加速度为g,求:
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内,管口B,C的连线水平.质量为m的带正电小球从B点正上方的A点自由下落A,B两点间距离为4R.从小球(小球直径小于细圆管直径)进人管口开始,整个空间中突然加上一个斜向左上方的匀强电场,小球所受电场力在竖直方向上的分力方向向上,大小与重力相等,结果小球从管口 C处离开圆管后,又能经过A点.设小球运动过程中电荷量没有改变,重力加速度为g,求: 如图所示,光滑绝缘的水平面上方,左边有垂直纸面向里的匀强磁场,右边有竖直向上的匀强电场.质量为m,带电量为q(正电)的点电荷 a,以水平向右的初速度v沿水平面进入匀强磁场和匀强电场,恰好都不脱离水平面.在匀强电场中用绝缘细线悬挂一个质量为m的不带电的小球b(可视为质点),小球处于静止且对水平面无压力.点电荷a进入匀强电场后与小球b正碰并粘在一起,恰好能绕悬挂点O在匀强电场中做竖直面内的圆周运动.(重力加速度为g)求:
如图所示,光滑绝缘的水平面上方,左边有垂直纸面向里的匀强磁场,右边有竖直向上的匀强电场.质量为m,带电量为q(正电)的点电荷 a,以水平向右的初速度v沿水平面进入匀强磁场和匀强电场,恰好都不脱离水平面.在匀强电场中用绝缘细线悬挂一个质量为m的不带电的小球b(可视为质点),小球处于静止且对水平面无压力.点电荷a进入匀强电场后与小球b正碰并粘在一起,恰好能绕悬挂点O在匀强电场中做竖直面内的圆周运动.(重力加速度为g)求: 如图所示,光滑绝缘的斜面倾角为37°,一带电量为+q的小物体质量为m,置于斜面上,当沿水平方向加一如图所示的匀强电场时,小物体恰好处于静止状态,从某时刻开始,电场强度突然减为原来的
如图所示,光滑绝缘的斜面倾角为37°,一带电量为+q的小物体质量为m,置于斜面上,当沿水平方向加一如图所示的匀强电场时,小物体恰好处于静止状态,从某时刻开始,电场强度突然减为原来的