题目内容

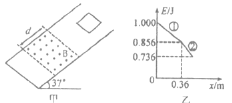
【题目】如图所示，在坚直平面内建立xo坐标系，曲线轨道OA部分的方程为y=x2在原点O处与x轴相切，A点的横坐标为0.6m；光滑圆弧轨道AB所对的圆心角为53°，半径R=1m。质量m=0.1kg、带电量g=2×10-5C的穿孔小球以3m/s的水平速度从O点进入轨道，以2m/s的速度从A端滑出后无碰撞地进入圆弧轨道。取g=10m/s2，求

（1）小球滑到圆弧轨道最低点B时对轨道的压力

（2）小球在OA轨道运动过程中克服摩擦力做的功

（3）要使小球在OA轨道运动过程中无机械能损失，可在空间施加一个电场。求场强的大小和方向？

【答案】（1）2.2N（2）0.65J （3）5×104N/C，方向竖直向下

【解析】

（1）A→B过程机械能守恒：

其中hAB=R-Rcos53°=0.4m

圆周B点处：FN-mg=m

联立解得FN=2.2N

根据牛顿第三定律，压力为2.2N，方向向下

（2）O→A过程，据动能定理：mghOA-Wf=

将xA=0.6代入y=得：yA=0.4m=hOA

解得：Wf=0.65J

（3））要使小球与OA轨道无挤压，须沿着y=轨迹运动

对照知a=20m/s2

竖直方向：mg+qE=ma

解得：E=5×104N/C，方向竖直向下

练习册系列答案
相关题目

【题目】2010年1月17日，我国成功发射北斗COMPASS-Gl地球同步卫星。这标志着中国北斗卫星导航系统工程建设又迈出重要一步。关于成功定点后的“北斗COMPASS-Gl”地球同步卫星，下列说法正确的是（ ）

A. 运行速度大于7.9 km/s

B. 离地面高度一定，相对地面静止

C. 绕地球运行的角速度比月球绕地球运行的角速度小

D. 向心加速度比静止在赤道上的物体的向心加速度大

【题目】有一固定轨道ABCD如图所示，AB段为四分之一的光滑圆弧轨道，其半径为R，BC段是水平光滑轨道，CD段是光滑斜面轨道，BC和斜面CD间用一小段光滑圆弧连接．有编号为1、2、3、4完全相同的4个小球（小球不能视为质点，其半径r＜R），紧挨在一起从圆轨道上某处由静止释放，经平面BC到斜面CD上，忽略一切阻力，则下列说法正确的是（ ）

A. 四个小球在整个运动过程中始终不分离

B. 在圆轨道上运动时，2号球对3号球不做功

C. 在CD斜面轨道上运动时，2号球对3号球做正功

D. 4号球在CD斜面轨道上运动的最大高度与1号球初始位置相同

【题目】下列说法正确的是(　 　)

A. β衰变释放出电子，说明原子核内有电子

B. 氡的半衰期为3.8天，8个氡原子核经过7.6天后剩下2个氡原子核

C. 原子核的比结合能越大，原子核越稳定

D. 用频率为ν的入射光照射光电管的阴极，遏止电压为Uc，改用频率为2ν的入射光照射同一光电管，遏止电压大于2Uc

【题目】如图甲所示，斜面倾角为θ=37°，一宽为d=0.65m的有界匀强磁场垂直于斜面向上，磁场边界与斜面底边平行。在斜面上由静止释放一矩形金属线框，线框沿斜面下滑，下边与磁场边界保持平行。取斜面底部为重力势能零势能面，从线框开始运动到恰好完全进入磁场的过程中，线框的机械能E和位移x之间的关系如图乙所示，图中①、②均为直线段。已知线框的质量为M=0.1 kg，电阻为R=0.06 Ω．（取g=l0m·s-2, sin 37°=0.6, cos 37°=0.8)求：

(1)线框与斜面间的动摩擦因数μ；

(2)线框刚进入磁场到恰好完全进入磁场所用的时间t：

(3)线框穿越磁场的过程中，线框中的最大电功率Pm。

【题目】如图甲所示，在坐标系xOy平面内，y轴的左侧有一个速度选择器，其中电场强度为E，磁感应强度为B0．粒子源不断地释放出沿x轴正方向运动，质量均为m、电量均为+q、速度大小不同的粒子．在y轴的右侧有一匀强磁场，磁感应强度大小恒为B，方向垂直于xOy平面，且随时间做周期性变化（不计其产生的电场对粒子的影响），规定垂直xOy平面向里的磁场方向为正，如图乙所示．在离y轴足够远的地方有一个与y轴平行的荧光屏．假设带电粒子在y轴右侧运动的时间达到磁场的一个变化周期之后，失去电荷变为中性粒子．（粒子的重力忽略不计）

（1）从O点射入右侧磁场的粒子速度多大；

（2）如果磁场的变化周期恒定为T=，要使不同时刻从原点O进入变化磁场的粒子做曲线运动的时间等于磁场的一个变化周期，则荧光屏离开y轴的距离至少多大；

（3）荧光屏离开y轴的距离满足（2）的前提下，如果磁场的变化周期T可以改变，试求从t=0时刻经过原点O的粒子打在荧光屏上的位置离x轴的距离与磁场变化周期T的关系．

【题目】如图所示是一种自动控制电路示意图，R1为光敏电阻，其阻值随光照强度的增大而减小。若发现电流表A中的电流突然减小，则光照强度I及a、b间的电压的变化情况是

A.I变大，U变大

B.I变大，U变小

C.I变小，U变大

D.I变小，U变小

【题目】某同学根据弹簧弹性势能的表达式（k为弹簧的劲度系数，x为弹簧的形变量）设计了如图所示的装置用来“探究做功与速度变化的关系”.将弹簧放置在水平气垫导轨上，左端固定，右端在O点，在O点右侧的B、C位置各安装一个光电门，计时器（图中未画出）与两个光电门相连，用带有遮光片的滑块压缩弹簧到某位置A，由静止释放。

（1）实验中，若A、O之间的距离x变为原来的2倍，则弹簧对滑块做的功为原来的_________倍；

（2）实验中，除了用米尺测量A、O之间的距离x，计时器显示遮光片从B到C所用的时间t外，_______（填“不需要”或“还需要”）测出B、C两点间距离s；

（3）实验中，若x与______（填“”或“”）成正比，则说明弹簧对滑块做的功与其速度的平方的变化成正比.

【题目】如图，一定质量的空气（可看成理想气体）被活塞封闭在竖直放置的圆柱形气缸内，汽缸壁导热良好，汽缸底部通过细管与打气筒连通；开始时活塞静止在汽缸中部，用打气筒缓慢充入压强为p0、体积为V0 = 84cm3的空气后，活塞缓慢上升h高度后静止；已知活塞的质量为m = 2kg，横截面积为S = 40cm2，气缸外大气压强为p0 = 1.0×105 Pa，温度为T0 = 300K，忽略活塞与气缸壁之间的摩擦，重力加速度g取10m/s2。

（1）求h的大小；

（2）逐渐升高外界的温度，同时往活塞的上表面倒入适量的沙子，使活塞保持不动。当外界的温度变为T = 320K时，倒入的沙子质量M为多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网