题目内容
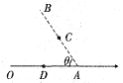
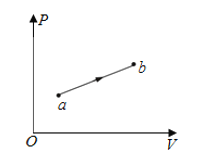
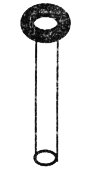
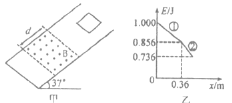
【题目】如图甲所示,斜面倾角为θ=37°,一宽为d=0.65m的有界匀强磁场垂直于斜面向上,磁场边界与斜面底边平行。在斜面上由静止释放一矩形金属线框,线框沿斜面下滑,下边与磁场边界保持平行。取斜面底部为重力势能零势能面,从线框开始运动到恰好完全进入磁场的过程中,线框的机械能E和位移x之间的关系如图乙所示,图中①、②均为直线段。已知线框的质量为M=0.1 kg,电阻为R=0.06 Ω.(取g=l0m·s-2, sin 37°=0.6, cos 37°=0.8)求:
(1)线框与斜面间的动摩擦因数μ;
(2)线框刚进入磁场到恰好完全进入磁场所用的时间t:
(3)线框穿越磁场的过程中,线框中的最大电功率Pm。
【答案】0.5;1/6s;0.54W
【解析】
(1)由能量守恒定律,线框减小的机械能等于克服摩擦力做功,则![]()
其中x1=0.36m;![]()
解得μ=0.5
(2)金属线框进入磁场的过程中,减小的机械能等于克服摩擦力和安培力做的功,机械能均匀减小,因此安培力也是恒力,线框做匀速运动,速度为v1
v12=2ax1
![]()
解得a=2m/s2 v1=1.2m/s
![]()
其中![]()
![]() x2为线框的侧边长,即线框进入磁场过程中运动的距离,可求出x2=0.2m,
x2为线框的侧边长,即线框进入磁场过程中运动的距离,可求出x2=0.2m,
则![]()
(3)线框刚出磁场时速度最大,线框内电功率最大![]()
由![]() 可求得v2=1.8m/s
可求得v2=1.8m/s
根据线框匀速进入磁场时:![]()
可得FA=0.2N
又因为![]()
可得![]()
将v2、B2L2带入可得:![]()

练习册系列答案
相关题目