Question

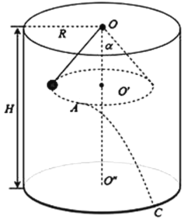
【题目】如图所示，在圆柱形仓库天花板中心的O点，挂一根L＝3m的细绳，绳的下端挂一个质量为m＝0.5kg的小球，已知绳能承受的最大拉力为10N。小球在水平面内做圆周运动，当小球速度逐渐增大时，细绳与竖直方向的夹角也随之变大。当速度逐渐增大某一数值，细绳正好断裂，设断裂时小球在图中的位置A，随后小球以v＝9m/s的速度正好落在墙角的C点。设g＝10m/s2，求：

（1）绳刚要断裂时与竖直方向夹角α及此时球做圆周运动的半径r；

（2）这个仓库屋顶的高度H和半径R。

Answer 1

【答案】（1）60°；m；（2）3.3m；4.8m

【解析】

(1)取小球为研究对象，设绳刚要断裂时拉力大小为F，则在竖直方向有

代入数据解得

α＝60°

球做圆周运动的半径

r＝Lsin60°＝

(2)OO′间的距离为

OO′＝Lcos60°＝1.5m

则O′O″间的距离为

O′O″＝H－OO′

由牛顿第二定律知

代入数据，可得

细绳断裂后小球做平抛运动，设A点在地面上的投影为B，如图所示

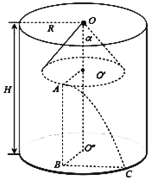
由运动的合成可知

由此可得小球平抛运动的时间

t＝0.6s

由平抛运动的规律可知小球在竖直方向上的位移

＝H－1.5m

所以屋的高度为

H＝＋1.5m＝3.3m

小球在水平方向上的位移为

x＝BC＝vAt＝m

由图可知圆柱形屋的半径为

R＝＝4.8m