题目内容
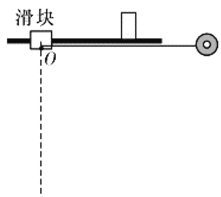
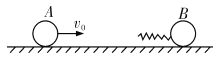
【题目】如图所示，在光滑水平面上，质量为m的小球B连接着一个轻质弹簧，弹簧与小球均处于静止状态。质量为3m的小球A以大小为
的水平速度向右运动，接触弹簧后逐渐压缩弹簧并使B运动，经过一段时间，A与弹簧分离。求：
(1)当弹簧压缩至最短时，弹簧的弹性势能
为多大；
(2)若开始时，在B球的右侧某位置固定一块挡板，在A与弹簧未分离前使B球与挡板发生碰撞，并在碰撞后立即将挡板撤走。设B球与挡板碰撞时间极短，碰后B球的速度大小不变，但方向与原来相反。欲使此后弹簧被压缩到最短时弹簧的弹性势能为第(1)问中的4倍，必须使两球在速度达到多大时与挡板发生碰撞。
【答案】(1)
；(2)A球速度为
，B球速度为
【解析】
(1)设弹簧压缩至最短时，A、B速度均为v，选择水平向右为正，根据动量守恒定律有
解得
根据机械能守恒定律有
解得
(2)弹簧被压缩到最短时弹簧的弹性势能
此时小球A、B的总动能
故小球A、B的总动量为0，B球与挡板碰撞前瞬间两球动量等大，设B球与挡板碰撞时，A球速度为大小
，B球速度为大小
根据动量守恒定律有
可得
，
练习册系列答案
相关题目
