题目内容
【题目】两轮平衡车（如图所示）广受年轻人的喜爱，它的动力系统由电池驱动，能够输出的最大功率为P0，小明驾驶平衡车在水平路面上沿直线运动，受到的阻力恒为Ff。已知小明和平衡车的总质量为m，从启动到达到最大速度的整个过程中，小明和平衡车可视为质点，不计小明对平衡车做的功。设平衡车启动后的一段时间内是由静止开始做加速度为a的匀加速直线运动，则（ ）
A.平衡车做匀加速直线运动过程中能达到的最大速度为v＝
B.平衡车运动过程中所需的最小牵引力为F＝Ff
C.平衡车达到最大速度所用的时间t＝
D.平衡车能达到的最大行驶速度v0＝
【答案】AB
【解析】
A．当平衡车的实际功率达到最大功率时匀加速直线运动速度达到最大值，则有：
根据牛顿第二定律可知：
联立可得平衡车做匀加速直线运动过程中能达到的最大速度为：
故A正确；
B．平衡车在运动过程中，根据牛顿第二定律可知：
即牵引力最小时即加速度为零时，因此
为最小值，故B正确；
C．启动后从静止到最大速度，平衡车先做匀加速直线运动，所用时间为：
之后平衡车做加速度减小的变加速运动，也需要一段时间，所以平衡车达到最大速度所用的时间大于
，故C错误；
D．平衡车所能达到的最大速度应该是合力为零时，即，可知最大速度为：
故D错误；
故选AB。
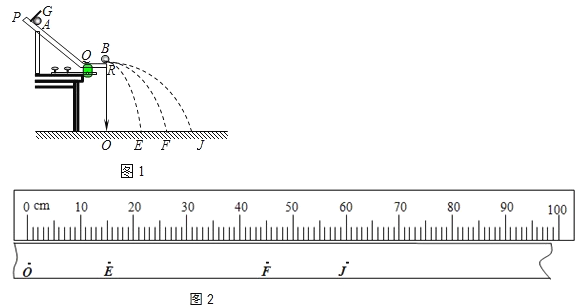
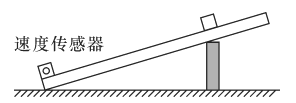
名校课堂系列答案
【题目】为验证动能定理，某同学设计了如下实验。将一长直木板一端垫起，另一端侧面装一速度传感器，让小滑块由静止从木板h高处（从速度传感器所在平面算起）自由下滑至速度传感器时，读出滑块经此处时的速度v，如图所示。多次改变滑块的下滑高度h（斜面的倾角不变），对应的速度值记录在表中：
下滑高度h/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
速度v/（m·s-1） | 0.633 | 0.895 | 1.100 | 1.265 | 1.414 |
要最简单直观地说明此过程动能定理是否成立，该同学建立了以h为纵轴的坐标系，你认为坐标系的横轴应该是___________，本实验是否需要平衡摩擦力___________（填“是”或“否”）。
