Question

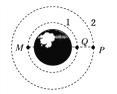
【题目】某同学设想驾驶一辆“陆地—太空”两用汽车(如图)，沿地球赤道行驶并且汽车相对于地球速度可以增加到足够大。当汽车速度增加到某一值时，它将成为脱离地面绕地球做圆周运动的“航天汽车”。不计空气阻力，已知地球的半径R＝6400km，重力加速度。下列说法正确的是 (　　)

A. 汽车在地面上速度增加时，它对地面的压力增大

B. 当汽车速度增加到8 km/s，将离开地面绕地球做圆周运动

C. 此“航天汽车”环绕地球做圆周运动的最小周期为1 h

D. 在此“航天汽车”上可以用弹簧测力计测量物体的重力

Answer 1

【答案】B

【解析】试题分析：汽车沿地球赤道行驶时，由重力和支持力的合力提供向心力，由牛顿第二定律分析速度减小时，支持力的变化，再由牛顿第三定律确定压力的变化．当速度增大时支持力为零，汽车将离开地面绕地球圆周运动．根据第一宇宙速度和地球半径求出“航天汽车”环绕地球做圆周运动的最小周期为1h．在此“航天汽车”上物体处于完全失重状态，不能用弹簧测力计测量物体的重力．

汽车沿地球赤道行驶时，由重力和支持力的合力提供向心力．设汽车的质量为m，支持力为F，速度为v，地球半径为R，则由牛顿第二定律得， ，当汽车速度v减小时，支持力F增大，则汽车对对地面的压力增大，故A错误；7.9km/s是第一宇宙速度，当汽车速度时，汽车将离开地面绕地球做圆周运动，成为近地卫星，故B正确；“航天汽车”环绕地球做圆周运动时半径越小，周期越小，则环绕地球附近做匀速圆周运动时，周期最小．
最小周期，v=7.9km/s，R=6400km，代入解得T=5087s=1.4h，“航天汽车”环绕地球做圆周运动的最小周期为1.4h，故C错误；在此“航天汽车”上物体处于完全失重状态，不能用弹簧测力计测量物体的重力，故D错误．