题目内容
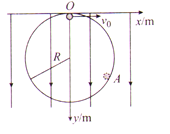
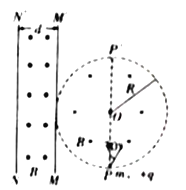
【题目】如图,以O点为圆心,半径为R的圆形区域内有垂直于纸面向内的匀强磁场,磁感应强度大小为B,线段![]() 是圆的一条直径,有一个质量为m、电荷量为+q的粒子在纸面内从P点射入磁场,射入磁场时速度方向与
是圆的一条直径,有一个质量为m、电荷量为+q的粒子在纸面内从P点射入磁场,射入磁场时速度方向与![]() 的夹角为30°,重力不计。
的夹角为30°,重力不计。
(1)若离子在![]() 点离开圆形磁场区域,求离子的速度大小
点离开圆形磁场区域,求离子的速度大小![]() ;
;
(2)现有大量该种离子,速率大小都是![]() ,在纸面内沿各个方向通过P点进入圆形磁场区域,试通过计算找出粒子只能在圆周的哪一步分射出圆形区域(不计粒子间相互作用);
,在纸面内沿各个方向通过P点进入圆形磁场区域,试通过计算找出粒子只能在圆周的哪一步分射出圆形区域(不计粒子间相互作用);
(3)若在圆形区域左侧还存在一个以![]() ,
,![]() 为边界的条形区域磁场,磁感应强度大小与圆形区域内相同,方向垂直纸面向外,两边界间距
为边界的条形区域磁场,磁感应强度大小与圆形区域内相同,方向垂直纸面向外,两边界间距![]() ,且有
,且有![]() ,其中
,其中![]() 与圆形区域相切,研究(2)问中离子的运动,求“射出圆形区域的位置”与P点相距最远的那些离子,它们从P点进入圆形区域直到离开条形区域所用的时间。
与圆形区域相切,研究(2)问中离子的运动,求“射出圆形区域的位置”与P点相距最远的那些离子,它们从P点进入圆形区域直到离开条形区域所用的时间。
【答案】(1) ![]() (2) 磁场圆上
(2) 磁场圆上![]() 个圆弧内;(3)
个圆弧内;(3) ![]()
【解析】试题分析:(1)根据左手定则得到粒子偏转方向,然后由几何关系求得圆周运动半径,即可由洛伦兹力做向心力求得粒子速度;(2)由洛伦兹力做向心力求得运动半径,即可由几何关系及粒子偏转方向求得出射区域;(3)根据几何关系就得粒子在圆形区域转过的中心角,然后由匀速直线运动规律求得在两磁场之间的运动时间;再由几何关系求得在条形区域转过的中心角,即可由洛伦兹力做向心力求得圆周运动周期,最后求得总的运动时间.
(1)粒子向左偏转,若离子在![]() 点离开圆形磁场区域
点离开圆形磁场区域
由几何关系得:粒子在磁场中做圆周运动的半径![]()
由洛伦兹力提供向心力,则有:![]()
解得:![]()
(2)由洛伦兹力提供向心力,则有: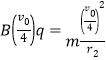
解得:粒子做圆周运动的半径![]()
粒子向左偏转,能到达的最远点的弦长![]()
记该点为Q,则![]()
即粒子只能只能在P到Q之间即圆形磁场区域P左侧![]() 个圆弧部分射出圆形区域
个圆弧部分射出圆形区域
(3)粒子在磁场中运动周期![]()
“射出圆形区域时的位置”与P点相距最远的那些离子,即从Q离开圆形磁场区域的离子在圆形磁场中转过中心角![]() ,所以运动时间
,所以运动时间![]()
离子从Q点离开圆心磁场时速度与![]() 成30°夹角,Q到
成30°夹角,Q到![]() 的距离
的距离![]()
则粒子离开圆形磁场到进入条形磁场的过程经历时间![]()
由左手定则可知粒子在条形磁场区域向粒子运动方向右侧偏转;粒子沿与![]() 成30°夹角的左下方进入条形磁场
成30°夹角的左下方进入条形磁场
因为![]() ,故粒子从
,故粒子从![]() 边界离开条形磁场区域
边界离开条形磁场区域
由几何关系得:粒子在条形磁场中转过的中心角![]()
故粒子在条形磁场中的运动时![]()
所以,粒子从P点进入圆形区域直到离开条形区域所用的时间![]()