题目内容
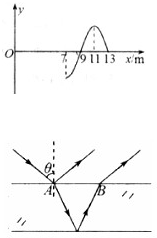 (1)位于坐标原点的波源S产生一列沿x轴正方向传播的简谐横波,波速v=40m/s,已知t=0时刻波刚好传播到x=13m处,部分波形如图所示.则波源S起振时的振动方向沿y轴
(1)位于坐标原点的波源S产生一列沿x轴正方向传播的简谐横波,波速v=40m/s,已知t=0时刻波刚好传播到x=13m处,部分波形如图所示.则波源S起振时的振动方向沿y轴(2)在实验室中,一位同学采用以下方式测出了镶嵌在某实验器材上的玻璃砖厚度:如图所示,让一束激光由空气射到玻璃砖表面上的A点,经下表面反射后,从上表面的B点射出,测得入射角为θ=45°,A、B两点间的距离为l=2cm,已知玻璃的折射率为n=
| 2 |
分析:根据波的传播方向可确定出x=13m处质点的振动方向,即为波源的起振方向.由图读出,由波速公式求出周期.
作出光路图,根据折射定律和反射定律以及几何知识,可求出玻璃砖的厚度d.
作出光路图,根据折射定律和反射定律以及几何知识,可求出玻璃砖的厚度d.
解答:解:(1)简谐横波沿x轴正方向传播,t=0时刻x=13m处的质点振动方向沿y轴正方向,
则波源S起振时的振动方向沿y轴正方向.
由图波长λ=8m,得到周期T=
=0.2
(2)设激光从上表面射入时的折射角为γ,
由折射定律,得
n=
由几何关系得到
sinγ=
解得
d=
=
cm
答:(1)正,0.2s
(2)玻璃砖的厚度d=
=
cm
则波源S起振时的振动方向沿y轴正方向.
由图波长λ=8m,得到周期T=
| λ |
| v |
(2)设激光从上表面射入时的折射角为γ,
由折射定律,得
n=
| sinθ |
| sinγ |
由几何关系得到
sinγ=
| ||||
|
解得
d=
L
| ||
| 2sinθ |
| 3 |
答:(1)正,0.2s
(2)玻璃砖的厚度d=
L
| ||
| 2sinθ |
| 3 |
点评:在波的图象问题中,由波的传播方向判断质点的振动方向是基本能力,波速公式也是一般知识,要熟练掌握和应用.

练习册系列答案
相关题目
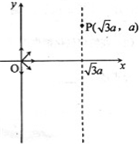 如图,在
如图,在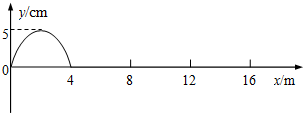 位于坐标原点的波源,在t=0时刻开始振动,起振的方向沿y轴负方向.产生的简谐横波沿x轴正方向传播,t=O.4s时刻,在0≤x≤4m区域内第一次出现如图所示的波形,则:
位于坐标原点的波源,在t=0时刻开始振动,起振的方向沿y轴负方向.产生的简谐横波沿x轴正方向传播,t=O.4s时刻,在0≤x≤4m区域内第一次出现如图所示的波形,则: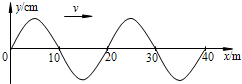 位于坐标原点的波源产生一列沿x轴正方向传播的简谐横波,在t=0时波源开始振动,经0.1s刚好传播到x=40m处第一次形成如图所示的波形.在x=400m处有一波的接收器(图中未画出),则下列说法正确的是( )
位于坐标原点的波源产生一列沿x轴正方向传播的简谐横波,在t=0时波源开始振动,经0.1s刚好传播到x=40m处第一次形成如图所示的波形.在x=400m处有一波的接收器(图中未画出),则下列说法正确的是( ) .求玻璃砖的厚度d. (结果可用根号表示)
.求玻璃砖的厚度d. (结果可用根号表示)