题目内容
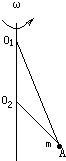
如图:直杆上O1O2两点间距为L,细线O1A长为
L,O2A长为L,A端小球质量为m,要使两根细线均被拉直,杆应以多大的角速度ω转动.
| 3 |

当ω较小时,线O1A拉直,O2A松弛;当ω较大时,线O2A拉直,O1A松弛.
设O2A刚好拉直,但FO2A又为零时,角速度为ω1,此时∠O2O1A=30°,对小球:
FO1A?cos30°=mg①
FO1A?sin30°=mω12
L?sin30°②
由①②解得ω1=
设O1A由拉紧转到刚被拉直,FO2A变为零时,角速度为ω2,对小球:
FO2A?cos60°=mg
FO2A?sin60°=mω22L?sin60°
解得ω2=
故杆转动的角速度范围为:
≤ω≤
.
答:要使两根细线均被拉直,杆的角速度范围为
≤ω≤
.
设O2A刚好拉直,但FO2A又为零时,角速度为ω1,此时∠O2O1A=30°,对小球:
FO1A?cos30°=mg①
FO1A?sin30°=mω12
| 3 |
由①②解得ω1=
|
设O1A由拉紧转到刚被拉直,FO2A变为零时,角速度为ω2,对小球:
FO2A?cos60°=mg
FO2A?sin60°=mω22L?sin60°
解得ω2=
|
故杆转动的角速度范围为:
|
|
答:要使两根细线均被拉直,杆的角速度范围为
|
|

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目