题目内容
【题目】如图所示，体积为V0的导热性能良好的容器中充有一定质量的理想气体，室温T0=300K。有一光滑导热活塞C（体积可忽略）将容器分成A、B两室，A室的体积是B室的3倍，B室内气体压强为大气压的1.5倍，左室容器中连接有一阀门K，可与大气相通（外界大气压等于P0）.
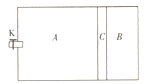
(i)将阀门K打开后，B室的体积变成多少？
( ii)打开阀门K后将容器内的气体从300K加热到900K，B室中气体压强变为多少？
【答案】
【解析】
①以B中气体为研究对象，应用玻意耳定律可以求出物体的体积．②应用盖吕萨克定律求出气体体积变为V0时气体的温度，然后应用查理定律求出气体的压强．
(1)B气体的初状态：
，
打开阀门，B室气体做做等温变化，
，体积为VB，
由玻意耳定律：pB0VB0=pBVB，
解得：
(2)温度从T0=300K升高到T，B中的气体由VB变化到V0，压强为pB，气体做等压变化，由盖吕萨克定律得：
，解得：T=800K，
故温度从800K升高到T1=9000K的过程中，气体做等容变化，
由查理定律得：
解得：
练习册系列答案
阅读快车系列答案
相关题目
