题目内容
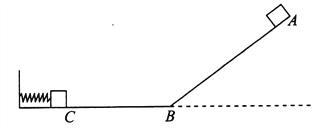
【题目】如图所示，有一自动卸煤矿车(可视为质点)沿如图所示轨道作业，其中AB段倾斜，与水平面夹角为37°，A点距水平面高度为12m，水平部分BC的长度为10.5m，AB与BC部分平滑连接，矿车与轨道间的动摩擦因数为0.3。一轻弹簧的左端固定在墙壁上，右端连接一底面光滑的重物静止在C点，其质量与装满煤的矿车的质量相等。现将装满煤的矿车从A点无初速度释放后，矿车沿轨道滑到C点时与重物发生弹性碰撞，然后矿车自动卸煤，卸煤后重物与矿车发生第二次碰撞(不考虑碰撞时的能量损失)，碰后矿车恰能到达轨道AB的中点处。已知重力加速度g=10m／s2，sin37°=0.6，求：
(1)矿车第一次经过B点时的速度；
(2)第一次碰撞结束瞬间重物的速度；
(3)矿车与所装煤的质量比(可用根式表示)。
【答案】(1)
；(2) 
，
；(3)
【解析】本题考查动能定理及物体的弹性碰撞。
（1）设矿车质量为
，所装煤的质量为
，矿车从A点下落到B点的速度为
，由动能定理可得
解得：
（2）设载煤矿车与重物碰撞前的速度为
，根据动能定理可得
重物与矿车相撞后，设矿车的速度为
，重物的速度为
由动量守恒定律得
由能量守恒定律得
联立解得：
、
（3）自动卸煤后重物与矿车发生第二次碰撞，碰撞后，设重物的速度为
，矿车的速度为
由动量守恒定律得
由能量守恒定律得
碰后矿车恰能达到轨道AB的中点，对矿车由动能定理可得
由以上各式解得：
练习册系列答案
相关题目
