题目内容
【题目】如图所示,PQ为一固定水平放置的光滑细长杆,质量均为m的两小球A、B穿于其上,两球被穿于杆上的轻弹簧相连.在A、B两球上还系有长度为2L的轻线,在轻线中间系有质量不计的光滑定滑轮E,C、D球质量分别为m和2m,用轻绳连接并跨过定滑轮.用手水平托住D球并保持D球静止状态,此时轻弹簧长度也为L,已知劲度系数为K,(弹簧在弹性限度内,重力加速度为g)求: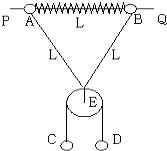
(1)人手对D球的支持力ND;
(2)连接A,B球的轻线上拉力大小T;
(3)长杆对A球的支持力大小NA;
(4)求弹簧的原始长度L0?
【答案】
(1)
解:C球处于静止状态,受力平衡,则绳上拉力大小F=mg,
D球在重力、绳子拉力以及人手对D球的支持力的作用下保持静止,根据平衡条件得:ND=2mg﹣F=mg
(2)
解:研究轻滑轮,轻滑轮处于平衡状态,受力分析如图,
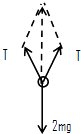
根据平衡条件得:2mg=Tcos30°×2
解得:T= ![]()
(3)
解:对A球进行受力分析,如图所示
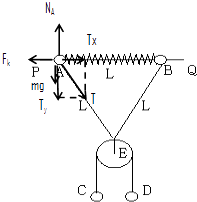
A球处于平衡状态,根据平衡条件得:
NA=Tcos30°+mg=2mg
(4)
解:A、B球在绳拉力作用下使弹簧处于压缩状态,
对A球受力分析可知,Fk=Tx
即k(L0﹣L)=Tsin30°
所以 ![]()
【解析】(1)C、D球都处于静止状态,受力平衡,分别对C、D受力分析,根据平衡条件列式求解;(2)研究轻滑轮,轻滑轮处于平衡状态,根据平衡条件求解;(3)对A球进行受力分析,A球处于平衡状态,根据平衡条件求出长杆对A球的支持力;(4)A、B球在绳拉力作用下使弹簧处于压缩状态,根据A球水平方向受力平衡,结合胡克定律求解.

练习册系列答案
相关题目