题目内容
(15分)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界均是边长为L的正方形(不计电子所受重力)。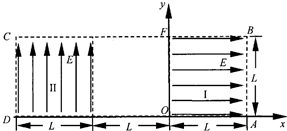
(1)在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置.
(2)在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置.
(3)若将左侧电场Ⅱ整体水平向右移动L/n(n≥1),仍使电子从ABCD区域左下角D处离开(D不随电场移动),求在电场Ⅰ区域内由静止释放电子的所有位置。
(1)电子离开ABCD区域的位置坐标为(-2L,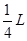 )(2)即在电场I区域内满足xy=
)(2)即在电场I区域内满足xy= 的函数的点即为所求位置。(3)即在电场I区域内满足该函数
的函数的点即为所求位置。(3)即在电场I区域内满足该函数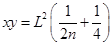 的点即为所求位置
的点即为所求位置
解析试题分析:(1)设电子的质量为m,电量为e,电子在电场I中做匀加速直线运动,出区域I时的速度为v0,此后在电场II中做类平抛运动,假设电子从CD边射出,出射点纵坐标为y,有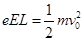

解得y=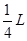
所以原假设成立,即电子离开ABCD区域的位置坐标为(-2L,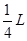 )
)
(2)设释放点在电场区域I中,其坐标为(x,y),在电场I中电子被加速到v1,然后进入电场II做类平抛运动,并从D点离开,有

解得xy= 即在电场I区域内满足该函数的点即为所求位置。
即在电场I区域内满足该函数的点即为所求位置。
(3)设电子从(x,y)点释放,在电场I中加速到v2,进入电场II后做类平抛运动,在高度为y′处离开电场II时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有
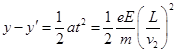
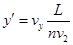
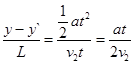
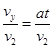
解得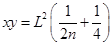
即在电场I区域内满足该函数的点即为所求位置
考点:本题考查动能定理、类平抛运动、数学知识在物理中的应用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
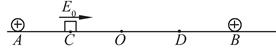
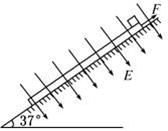
 kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,重力加速度取g=10m/s2,sin37o=0.6,cos37o=0.8。(计算结果可保留根号)求:
kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,重力加速度取g=10m/s2,sin37o=0.6,cos37o=0.8。(计算结果可保留根号)求: 

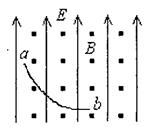

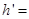 2.5m,求小球在半圆轨道上克服摩擦力所做的功.
2.5m,求小球在半圆轨道上克服摩擦力所做的功.