题目内容
(12分)如图所示,在倾角为37o的斜面上,一劲度系数为k=100N/m的轻弹簧一端固定在A点,自然状态时另一端位于B点。斜面上方有一半径R=0.2m、圆心角等于143°的竖直圆弧形光滑轨道与斜面相切于C处,圆弧轨道的最高点为D。斜面AB段光滑,BC段粗糙且长度为0.4m。现将一质量为1kg的小物块从C点由静止释放,小物块将弹簧压缩了0.2m后速度减为零(不计小物块到达B处与弹簧碰撞时的能量损失)。已知弹簧弹性势能表达式Ek= kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,重力加速度取g=10m/s2,sin37o=0.6,cos37o=0.8。(计算结果可保留根号)求:
kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,重力加速度取g=10m/s2,sin37o=0.6,cos37o=0.8。(计算结果可保留根号)求: 
⑴小物块与斜面BC段间的动摩擦因数μ
⑵小物块第一次返回BC面上时,冲到最远点E,求BE长
⑶若用小物块将弹簧压缩,然后释放,要使小物块在CD段圆弧轨道上运动且不脱离圆弧轨道,则压缩时压缩量应满足的条件
⑴μ=0.5 ⑵0.08m的E位置 ⑶x≥0.479m
解析试题分析:⑴由动能定理得: 2分
2分
解得:μ="0.5" 1分
⑵设小物块最远将冲到E点,则由动能定理得: 2分
2分
解得:BE=0.08m,即最远冲到距B点为0.08m的E位置。 1分
⑶要使小物块不脱离圆弧轨道,则小物块应到达图中F点时速度减为零则有: >0 1分
>0 1分 ≤0 1分
≤0 1分
解得: <x≤
<x≤ 即:0.349m<x≤0.4m 1分
即:0.349m<x≤0.4m 1分
若恰过最高点D,则有: ≥
≥ mv2 1分
mv2 1分
mg= m 1分
1分
解得: x≥ 即:x≥0.479m 1分
即:x≥0.479m 1分
考点:本题考查动能定理、圆周运动。

练习册系列答案
相关题目
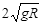 。求:
。求:
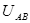 ;
;
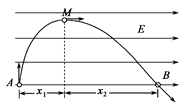
 。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3,如图所示。空气和桌面对物体的阻力均忽略不计。
。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3,如图所示。空气和桌面对物体的阻力均忽略不计。
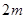 的木板A静止在光滑水平面上,其右端与固定挡板相距
的木板A静止在光滑水平面上,其右端与固定挡板相距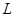 ,内壁光滑的弹射器利用压缩弹簧把质量为
,内壁光滑的弹射器利用压缩弹簧把质量为 的物块B(视为质点)水平向右弹射出去,B弹出后从A左端的上表面水平滑入,之后立刻拿走弹射器。已知A足够长,B不会从A表面滑出,A与挡板的碰撞无机械能损失;弹射器弹簧储存的弹性势能为
的物块B(视为质点)水平向右弹射出去,B弹出后从A左端的上表面水平滑入,之后立刻拿走弹射器。已知A足够长,B不会从A表面滑出,A与挡板的碰撞无机械能损失;弹射器弹簧储存的弹性势能为 ,重力加速度为
,重力加速度为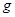 ,不计空气阻力。
,不计空气阻力。


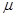 满足的条件。
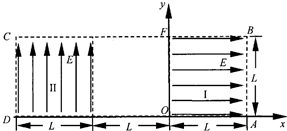
满足的条件。 的电场加速后,从C点沿水平方向飞入电场强度为
的电场加速后,从C点沿水平方向飞入电场强度为 的匀强电场中,到达该电场中另一点D时,电子的速度方向与电场强度方向的夹角正好是120°,如图所示。试求C、D两点沿电场强度方向的距离y。
的匀强电场中,到达该电场中另一点D时,电子的速度方向与电场强度方向的夹角正好是120°,如图所示。试求C、D两点沿电场强度方向的距离y。

 。
。