题目内容
坐标原点O处有一点状的放射源,它向xOy平面内的x轴上方各个方向发射α粒子,α粒子的速度大小都是v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为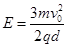 ,其中q与m分别为α粒子的电荷量和质量;在d<y<2d的区域内分布有垂直于xOy平面的匀强磁场.ab为一块很大的平面感光板,放置于y=2d处,如图所示.观察发现此时恰无粒子打到ab板上.(不考虑α粒子的重力)
,其中q与m分别为α粒子的电荷量和质量;在d<y<2d的区域内分布有垂直于xOy平面的匀强磁场.ab为一块很大的平面感光板,放置于y=2d处,如图所示.观察发现此时恰无粒子打到ab板上.(不考虑α粒子的重力)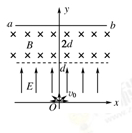
(1)求α粒子刚进入磁场时的动能;
(2)求磁感应强度B的大小;
(3)将ab板平移到什么位置时所有粒子均能打到板上?并求出此时ab板上被α粒子打中的区域的长度.
(1)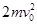 ;(2)
;(2)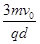 ;(3)
;(3)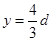 ; (3)
; (3)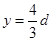 ;
;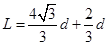
解析试题分析:(1)根据动能定理:Eqd= mv2-
mv2- mv
mv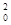 ,则末动能为Ek=
,则末动能为Ek= mv2=Eqd+
mv2=Eqd+ mv
mv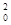 =2mv
=2mv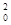 .
.
(2)根据(1)中结果可知v=2v0,对于沿x轴正方向射出的粒子进入磁场时与x轴正方向夹角θ=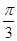 ,其在电场中沿x轴方向的位移x1=v0t=
,其在电场中沿x轴方向的位移x1=v0t=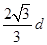 .该粒子运动轨迹如图所示,根据几何知识可知:若该粒子不能打到ab板上,则所有粒子均不能打到ab板上,因此该粒子轨迹必与ab板相切,其圆周运动的半径满足关系式d=r+rcos 60°,则r=
.该粒子运动轨迹如图所示,根据几何知识可知:若该粒子不能打到ab板上,则所有粒子均不能打到ab板上,因此该粒子轨迹必与ab板相切,其圆周运动的半径满足关系式d=r+rcos 60°,则r=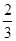 d,又根据洛伦兹力提供向心力Bqv=
d,又根据洛伦兹力提供向心力Bqv=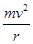 ,可得
,可得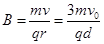
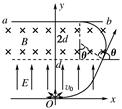
(3)根据几何知识可知,沿x轴负方向射出的粒子若能打到ab板上,则所有粒子均能打到ab板上.其临界情况就是此粒子轨迹恰好与ab板相切.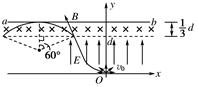
由图可知此时磁场宽度应为原来的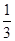 ,即当ab板位于y=
,即当ab板位于y=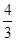 d的位置时,恰好所有粒子均能打到板上,且ab板上被打中区域的长度为L=2x1+r=
d的位置时,恰好所有粒子均能打到板上,且ab板上被打中区域的长度为L=2x1+r=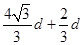 .
.
考点: 带电粒子在磁场中的运动

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
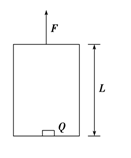
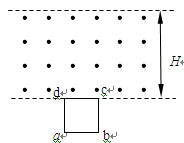
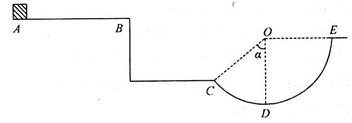
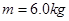 的滑块(可视为质点),在F=60N的水平拉力作用下从A点由静止开始运动,一段时间后撤去拉力F,当滑块由平台边缘B点飞出后,恰能从水平地面上的C点沿切线方向落入竖直圆弧轨道CDE,并从轨道边缘E点竖直向上飞出,经过0.4 s后落回E点。已知AB间的距离L="2.3" m,滑块与平台间的动摩擦因数
的滑块(可视为质点),在F=60N的水平拉力作用下从A点由静止开始运动,一段时间后撤去拉力F,当滑块由平台边缘B点飞出后,恰能从水平地面上的C点沿切线方向落入竖直圆弧轨道CDE,并从轨道边缘E点竖直向上飞出,经过0.4 s后落回E点。已知AB间的距离L="2.3" m,滑块与平台间的动摩擦因数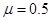 ,平台离地高度
,平台离地高度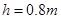 ,B、C两点间水平距离s="1.2" m,圆弧轨道半径R=1.0m。重力加速度g取10 m/s2,不计空气阻力。求:
,B、C两点间水平距离s="1.2" m,圆弧轨道半径R=1.0m。重力加速度g取10 m/s2,不计空气阻力。求: