Question

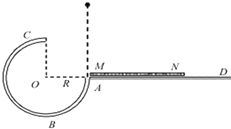
【题目】如图所示，一个3/4圆弧形光滑圆管轨道ABC,放置在竖直平面内，轨道半径为R，在A点与水平地面AD相接，地面与圆心O等高，MN 是放在水平地面上长为3R、厚度不计的减振垫，左端M正好位于A点．一个质量为m的小球从A处管口正上方某处由静止释放，若不考虑空气阻力，小球可看作质点，那么以下说法中正确的是（ ）

A．要使球能从C点射出后能打到垫子上，则球经过C点时的速度至少为

B．要使球能从C点射出后能打到垫子上，则球经过C点时的速度至少为

C．若球从C点射出后恰好能打到垫子的M端，则球经过C点时对管的作用力大小为mg/2 ，方向向下

D．要使球能通过C点落到垫子上，球离A点的最大高度是5R

Answer 1

【答案】BCD

【解析】

试题分析：要使球能从C点射出后能打到垫子上，从C点开始做平抛运动，竖直分位移为R，水平分位移设为x，故有：R=gt2；x=vCt, 其中：4R≥x≥R，解得：，即球经过C点时的速度至少为．故A错误，B正确；若球从C点射出后恰好能打到垫子的M端，由上知，球在C点的速度为；在C点，重力和支持力的合力提供向心力，设支持力向下，根据牛顿第二定律，有：

解得：N=-mg，负号表示N的方向向上；根据牛顿第三定律知，球对管的作用力大小大小为mg，方向向下．故C正确．要使球能通过C点落到垫子上N点，球离A点的高度最大，由上可知球在C点的速度为，根据动能定理，有：mgh=mgR+mvC2，解得：h=5R，故D正确．故选BCD．