Question

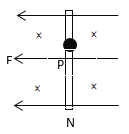
【题目】如图，水平面上有两根足够长的光滑平行金属导轨，导轨间距为l，电阻不计。左侧接有定值电阻R。质量为m、电阻为r的导体杆，以初速度v0沿轨道滑行，在滑行过程中保持与轨道垂直且接触良好。整个装置处于方向竖直向上，磁感应强度为B的匀强磁场中。宏观规律与微观规律有很多相似之处，导体杆速度的减小规律类似于放射性元素的半衰期，理论上它将经过无限长的时间衰减完有限的速度。

（1）求在杆的速度从v0减小到的过程中

a.电阻R上产生的热量

b.通过电阻R的电量

（2）a．证明杆的速度每减小一半所用的时间都相等

b.若杆的动能减小一半所用时间为t0，则杆的动量减小一半所用时间是多少?

Answer 1

【答案】（1）a. b. （2）a. a.某时刻杆的速度为v（从v0开始分析亦可），则感应电动势E=Blv，感应电流，安培力,在很短时间内，由动量定理，（为速度变化绝对值）可得,所以在任意短时间内速度变化的比例为,由于为定值，所以任何相等时间内速度变化的比例都相等。所以从任何时刻开始计算，速度减小一半所用时间都相等。 b.2t0

【解析】

（1）a.设电路产热为Q，由能量守恒+Q

串联电路中，产热与电阻成正比，可得

解得电阻R产热为

b.设该过程所用时间为t，由动量定理：，其中

解得通过R的电量为

（2）a.某时刻杆的速度为v（从v0开始分析亦可），则

感应电动势E=Blv，

感应电流，

安培力

在很短时间内，由动量定理，（为速度变化绝对值）

可得

所以在任意短时间内速度变化的比例为

由于为定值，所以任何相等时间内速度变化的比例都相等。

所以从任何时刻开始计算，速度减小一半所用时间都相等。

b.动能减小一半，速度v减小为

由a中分析可得，速度从再减小到所用时间仍为t0

所以速度减小一半所用时间为2t0，动量减小一半所有时间也为2t0。