题目内容
11.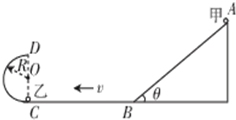 如图所示,ABCD为竖直平面内固定的光滑轨道,其中AB为斜面,BC段是水平的,CD段为半径R=0.2m的半圆,圆心为O,与水平面相切与C点,直径CD垂直于BC.现将小球甲从斜面上距BC高为10R/3的A点由静止释放,到达B点后只保留水平速度沿水平面运动,与静止在C点点小球乙发生弹性碰撞.已知甲、乙两球队质量均为m=0.01kg,重力加速度g取10m/s2.(水平轨道足够长,甲、乙两球可视为质点)求:
如图所示,ABCD为竖直平面内固定的光滑轨道,其中AB为斜面,BC段是水平的,CD段为半径R=0.2m的半圆,圆心为O,与水平面相切与C点,直径CD垂直于BC.现将小球甲从斜面上距BC高为10R/3的A点由静止释放,到达B点后只保留水平速度沿水平面运动,与静止在C点点小球乙发生弹性碰撞.已知甲、乙两球队质量均为m=0.01kg,重力加速度g取10m/s2.(水平轨道足够长,甲、乙两球可视为质点)求:(1)甲乙两球碰撞后,乙恰好能通过轨道的最高点D,则甲、乙碰后瞬间,乙对轨道最低点C处的压力F;
(2)在满足(1)的条件下,求斜面与水平面的夹角
(3)若将甲仍从A点释放,增大甲的质量,保持乙的质量不变,求能让乙通过D点速度范围.
分析 (1)首先小球乙为研究对象,乙恰能通过轨道的最高点D,则重力恰好通过向心力,列出牛顿第二定律的方程;从C到D的过程中,小球乙的机械能守恒,列出方程,联立即可求出小球在C的速度,最后使用牛顿第二定律求出小球在C处受到的支持力,由牛顿第三定律说明即可.
(2)利用机械能守恒求出甲到达B点的速度,然后将速度分解,保留水平方向的分速度即为C点的速度;甲与乙碰撞的过程中动量守恒,能量守恒,联立方程即可求出斜面的倾角.
(3)增大甲的质量,保持乙的质量不变,则甲乙碰撞的过程中乙获得的速度增大,然后由机械能守恒求出小球乙D点的速度范围.
解答 解:(1)乙恰能通过轨道的最高点D,则重力恰好通过向心力,得:$mg=\frac{m{v}_{D}^{2}}{R}$
乙球从C到D的过程中机械能守恒,得:$\frac{1}{2}m{v}_{C}^{2}=2mgR+\frac{1}{2}m{v}_{D}^{2}$
联立以上两式得:${v}_{C}=\sqrt{5gR}$
乙球在C点受到的支持力与重力的合力提供向心加速度,得:${F}_{N}-mg=\frac{m{v}_{C}^{2}}{R}$
所以:${F}_{N}=mg+\frac{m{v}_{C}^{2}}{R}$=6×1.0×10-2N=0.6N
由牛顿第三定律可知,乙对半圆轨道最低点C处的压力与轨道对小球的支持力大小相等,即:F=FN=0.6N
(2)甲与乙的质量相同,所以甲与乙发生弹性碰撞的过程二者交换速度,所以甲到达C的速度等于乙在C点的速度,即:${v}_{甲x}={v}_{C}=\sqrt{5gR}$
甲从A滑到B的过程中机械能守恒,得:mgh=$\frac{1}{2}m{v}^{2}$
甲到达B点后只保留水平分速度沿水平面运动,则:v甲x=v•cosθ
所以:$cosθ=\frac{{v}_{甲x}}{v}$=$\frac{\sqrt{5gR}}{\sqrt{2gh}}=\frac{\sqrt{5gR}}{\sqrt{2g×\frac{10R}{3}}}=\frac{\sqrt{3}}{2}$
则:θ=30°
(3)将甲仍从A点释放,增大甲的质量为M,甲到达C的速度仍然是$\sqrt{5gR}$,保持乙的质量不变,仍然发生弹性碰撞,以向左为正方向,则:
动量守恒:MvC=Mv1+mv2
机械能守恒:$\frac{1}{2}M{v}_{C}^{2}=\frac{1}{2}M{v}_{1}^{2}+\frac{1}{2}m{v}_{2}^{2}$
联立解得:${v}_{1}=\frac{(M-m){v}_{C}}{M+m}$,${v}_{2}=\frac{2M{v}_{C}}{M+m}$
若增大甲的质量,保持乙的质量不变,m甲≥m,则得 v≤v乙<2v
当v乙=v=$\sqrt{10}$m/s时,乙球通过D的速度为vD=$\sqrt{gR}$=$\sqrt{10×0.2}$=$\sqrt{2}$m/s
当v乙=2v=2$\sqrt{10}$m/s时,由机械能守恒得
2mgR+$\frac{1}{2}$mvD2=$\frac{1}{2}$mv乙2
解得 vD=4$\sqrt{2}$m/s
范围为$\sqrt{2}$m/s≤vD<4$\sqrt{2}$m/s
答:(1)甲、乙碰后瞬间,乙对半圆轨道最低点C处的压力是0.6N;
(2)斜面与水平面的夹角是30°;
(3)能让乙通过D点速度范围为$\sqrt{2}$m/s≤vD<4$\sqrt{2}$m/s
点评 本题关键是明确两个小球的运动情况,然后分过程运用机械能守恒定律、动量守恒定律、平抛运动的分位移公式和向心力公式列式求解.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案 如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )
如图所示,虚线a、b、c代表电场中的三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,据此可知( )| A. | 带电质点通过P点时的电势能较Q点小 | |
| B. | 三个等势面中,c的电势最高 | |
| C. | 带电质点通过P点时的动能较Q点大 | |
| D. | 带电质点通过P点时的加速度较Q点大 |
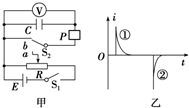 某同学设计了一个探究电容器所带电荷量与电容器两极板间电压关系的实验,实验电路如图甲所示,其中P为电流传感器,V为理想电压表.实验时,先将开关S1闭合,单刀双掷开关S2掷向a,调节滑动变阻器的滑动头到某位置使电容器C充电,当电路稳定后记录理想电压表的示数.再迅速将开关S2掷向b,使电容器放电.电流传感器P将电容器充、放电过程中的电流数据传送给计算机,在计算机上可显示出电流i随时间t变化的图象如图乙所示.然后改变滑动变阻器滑动头的位置,重复上述步骤,记录多组电流随时间变化的图象和电压表的示数.对于这个实验过程和由图象及数据所得出的结果,下列说法中正确的是( )
某同学设计了一个探究电容器所带电荷量与电容器两极板间电压关系的实验,实验电路如图甲所示,其中P为电流传感器,V为理想电压表.实验时,先将开关S1闭合,单刀双掷开关S2掷向a,调节滑动变阻器的滑动头到某位置使电容器C充电,当电路稳定后记录理想电压表的示数.再迅速将开关S2掷向b,使电容器放电.电流传感器P将电容器充、放电过程中的电流数据传送给计算机,在计算机上可显示出电流i随时间t变化的图象如图乙所示.然后改变滑动变阻器滑动头的位置,重复上述步骤,记录多组电流随时间变化的图象和电压表的示数.对于这个实验过程和由图象及数据所得出的结果,下列说法中正确的是( )| A. | 流过电流传感器P的充电电流和放电电流方向相同 | |
| B. | 图乙中的第①段(充电阶段)电流曲线与横轴所围图形的面积表示电容器充电结束时所带的电荷量 | |
| C. | 电容器所带电荷量与电容器两极板间电压的关系图象应为一条过原点的倾斜直线 | |
| D. | 电容器充电结束时所带电荷量与滑动变阻器滑动头的位置无关 |
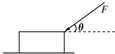 质量为m的木块,在与水平方向夹角为θ的推力F作用下,沿水平地面做匀速运动,如右图所示,已知木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力应为( )
质量为m的木块,在与水平方向夹角为θ的推力F作用下,沿水平地面做匀速运动,如右图所示,已知木块与地面间的动摩擦因数为μ,那么木块受到的滑动摩擦力应为( )| A. | μmg | B. | μ(mg+Fsin θ) | C. | μ(mg-Fsin θ) | D. | Fcos θ |
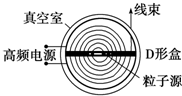
| A. | 它们的最大速度相同 | |
| B. | 它们的最大动能相同 | |
| C. | 加速氘核${\;}_{1}^{2}$H时高频电源的频率大于加速氦核${\;}_{2}^{4}$He的频率 | |
| D. | 加速氘核${\;}_{1}^{2}$H时高频电源的频率小于加速氦核${\;}_{2}^{4}$He的频率 |
| A. | 重力势能只由重物决定 | |
| B. | 重力势能不能有负值 | |
| C. | 重力势能的大小是绝对的 | |
| D. | 物体克服重力做功等于重力势能的增加 |
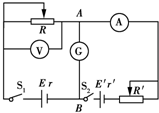 某同学设计了如图所示的电路,该电路能够测量电源E的电动势和内电阻r,E′是辅助电源.A、B两点间有一灵敏电流计G.
某同学设计了如图所示的电路,该电路能够测量电源E的电动势和内电阻r,E′是辅助电源.A、B两点间有一灵敏电流计G.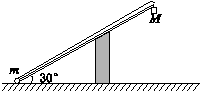 如图所示,长为L,内壁光滑的直管 与水平地面成30°角固定放置,将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km(k>2)的小物块相连,小物块悬挂于管口,现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球的转向过程中速率不变.(重力加速度为g)
如图所示,长为L,内壁光滑的直管 与水平地面成30°角固定放置,将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=km(k>2)的小物块相连,小物块悬挂于管口,现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球的转向过程中速率不变.(重力加速度为g)