题目内容
17. 在均匀介质中选取平衡位置在同一直线上的9个质点,相邻两质点间的距离均为L,如图甲所示.一列横波沿该直线向右传播,t=0时到达质点1,质点1开始向下运动,经过时间△t第一次出现如图乙所示的波形.求:
在均匀介质中选取平衡位置在同一直线上的9个质点,相邻两质点间的距离均为L,如图甲所示.一列横波沿该直线向右传播,t=0时到达质点1,质点1开始向下运动,经过时间△t第一次出现如图乙所示的波形.求:(1)该波的波长;
(2)质点振动的周期;
(3)该波的波速.
分析 由图确定波长,t=0时到达质点1,质点1开始向下运动,则介质中所有质点起振方向均向下.图b中质点9此刻振动方向向上,说明波不是才传到质点9,而是传到9后又经过了$\frac{1}{2}$ 周期,则时间△t与周期的关系为△t=1.5T,求出周期,再由波速公式求解波速
解答 解:(1)由图读出波长λ=8L,
(2)横波沿该直线向右传播,图示时刻质点9的振动方向向上.由题波源1的起振动方向向下,则第一次出现如图乙所示的波形,振动传到质点9后,又传播了$\frac{1}{2}$周期,则时间△t与周期的关系为△t=1.5T,T=$\frac{2}{3}△t$
(3)波速v=$\frac{λ}{T}$=$\frac{12L}{△t}$
答:(1)该波的波长8L;
(2)质点振动的周期$\frac{2}{3}△t$;
(3)该波的波速$\frac{12L}{△t}$
点评 本题考查分析波动形成过程的能力,关键在于分析如何第一次形成图示波形.容易犯的错误是认为T=△t,这样质点9的起振方向与波源的起振方向将不一致

练习册系列答案
相关题目
7.一物体静止在粗糙水平地面上,现用一个大小为F1的水平拉力拉动物体,经过一段时间后其速度变为v,若将水平拉力的大小改为F2,物体从静止开始经过同样的时间后速度变为3v,对于上述两个过程,用WF1、WF2分别表示拉力F1,F2所做的功,Wf1、Wf2分别表示前后两次克服摩擦力所做的功,则( )
| A. | WF2>9WF1,Wf2>3Wf1 | B. | WF2<9WF1,Wf2=3Wf1 | ||
| C. | WF2>9WF1,Wf2=3Wf1 | D. | WF2<9WF1,Wf2<3Wf1 |
8.下列说法正确的是( )
| A. | 物体的加速度大,则速度也一定大 | |
| B. | 物体的速度变化越快,则加速度越大 | |
| C. | 物体的速度大,速度变化就越大,则加速度也越大 | |
| D. | 物体速度很大,加速度可能为零;加速度很大,速度不可能为零 |
5.做直线运动的物体,在第1末、第2末、第3末的速度分别是1m/s,2m/s,3m/s,则物体的运动性质是( )
| A. | 一定是匀变速直线运动 | |
| B. | 一定是非匀变速直线运动 | |
| C. | 加速度不断增大的直线运动 | |
| D. | 可能是匀变速,也可能是非匀变速运动 |
2. 如图所示,在光滑水平面上有一个竖直向上的匀强磁场,分布在宽度为l的区域内.现有一个边长为a的正方形闭合导线框(a<l),以初速度v0垂直于磁场边界沿水平面向右滑过该磁场区域,滑出时的速度为v.下列说法中正确的是( )
如图所示,在光滑水平面上有一个竖直向上的匀强磁场,分布在宽度为l的区域内.现有一个边长为a的正方形闭合导线框(a<l),以初速度v0垂直于磁场边界沿水平面向右滑过该磁场区域,滑出时的速度为v.下列说法中正确的是( )
 如图所示,在光滑水平面上有一个竖直向上的匀强磁场,分布在宽度为l的区域内.现有一个边长为a的正方形闭合导线框(a<l),以初速度v0垂直于磁场边界沿水平面向右滑过该磁场区域,滑出时的速度为v.下列说法中正确的是( )
如图所示,在光滑水平面上有一个竖直向上的匀强磁场,分布在宽度为l的区域内.现有一个边长为a的正方形闭合导线框(a<l),以初速度v0垂直于磁场边界沿水平面向右滑过该磁场区域,滑出时的速度为v.下列说法中正确的是( )| A. | 导线框完全进入磁场中时,速度大于$\frac{({v}_{0}+v)}{2}$ | |
| B. | 导线框完全进入磁场中时,速度等于$\frac{({v}_{0}+v)}{2}$ | |
| C. | 导线框完全进入磁场中时,速度小于$\frac{({v}_{0}+v)}{2}$ | |
| D. | 以上三种都有可能 |
9.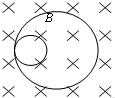 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了某种衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,有( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了某种衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,有( )
 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了某种衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,有( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了某种衰变而形成了如图所示的两个圆形径迹,两圆半径之比为1:16,有( )| A. | 该原子核发生了α衰变 | |
| B. | 该原子核发生了β衰变 | |
| C. | 那个打出衰变粒子的反冲核沿小圆作逆时针方向运动 | |
| D. | 该衰变过程结束后其系统的总质量略有增加 |
7.关于运动的合成和分解,下述说法中正确的是( )
| A. | 合运动的速度大小可以小于任何一个分速度的大小 | |
| B. | 物体的两个分运动若是直线运动,则它的合运动一定是直线运动 | |
| C. | 合运动和分运动具有等时性 | |
| D. | 若合运动是曲线运动,则其分运动中至少有一个是曲线运动 |
 如图所示,两个相同的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在同一点O,并用长度相同的细线连接A、B两小球,然后,用一水平方向的力F作用在小球A上,此时三根细线均处于直线状态,且OB细线恰好处于竖直方向,不考虑小球的大小,两小球均处于静止状态,则
如图所示,两个相同的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在同一点O,并用长度相同的细线连接A、B两小球,然后,用一水平方向的力F作用在小球A上,此时三根细线均处于直线状态,且OB细线恰好处于竖直方向,不考虑小球的大小,两小球均处于静止状态,则
