题目内容
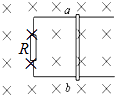
【题目】如图所示，A板发出的电子经加速后，水平射入水平放置的两平行金属板间，金属板间所加的电压为U，电子最终打在荧光屏P上，关于电子的运动，下列说法中正确的是（ ）
A.滑动触头向右移动时，电子打在荧光屏上的位置上升
B.滑动触头向左移动时，电子打在荧光屏上的位置上升
C.电压U增大时，电子打在荧光屏上的速度大小不变
D.电压U增大时，电子从发出到打在荧光屏上的时间不变
【答案】B,D
【解析】解：电子在加速电场中做加速运动，根据动能定理得：eU′= 
mv2﹣0，则得电子获得的速度为：v= 
．
电子进入偏转电场后做类平抛运动，电子在沿极板方向做匀速直线运动，粒子在电场中运动时间：t= 
；
在平行电场方向做初速度为0的匀加速直线运动，加速度a= 
，电子在电场方向偏转的位移y= at2．
解得：y= 
，又因为偏转电场方向向下，所以电子在偏转电场里向上偏转．
A、滑动触头向右移动时，加速电压U′变大，由上可知电子偏转位移变小，因为电子向上偏转，故在屏上的位置下降，相反，滑动触头向左移动时，电子打在荧光屏上的位置上升，故A错误，B正确；
C、偏转电压U增大时，电子在电场中受到的电场力增大，即电子偏转的加速度a增大，又因为电子加速获得的速度v不变，电子在电场中运动的时间不变，a增大，而电子打在屏上的速度为v′= 
，故电子打在屏上的速度增大，故C错误．
D、电子在电场中运动的时间不变，离开电场后做匀速直线运动，由于水平速度不变，运动时间也不变，所以电子从发出到打在荧光屏上的时间不变，故D正确．
故选：BD．
滑动触头向右移动时，加速电压增大，加速后速度变大，粒子在偏转电场中运动时间变短，粒子在平行偏转电场方向的位移减小．同理触头向左移动时，加速电压减小，加速后速度变小，粒子在电场中运动时间变长，粒子在平行偏转电场方向的位移增大；当加速电压不变时，偏转电压变化，影响平行电场方向的电场力的大小，也就是影响加速度的大小，粒子在电场中运动时间不变，改变偏转的位移大小．
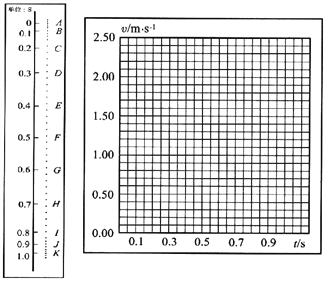
【题目】利用打点计时器研究一个约1.4m高的商店卷帘窗的运动.将纸带粘在卷帘底部，纸带通过打点计时器随帘在竖直面内向上运动.打印后的纸带如下图所示，数据如表格所示.纸带中AB、BC、CD……每两点之间的时间间隔为0.10s，根据各间距的长度，可计算出卷帘窗在各间距内的平均速度v平均.可以将v平均近似地作为该间距中间时刻的即时速度v.
(1)请根据所提供的纸带和数据，绘出卷帘窗运动的v-t图像.
(2)AD段的加速度为______m／s2，AK段的平均速度为______m／s.
卷帘运动数据
间隔 | 间距 (cm) |
AB | 5.0 |
BC | 10.0 |
CD | 15.0 |
DE | 20.0 |
EF | 20.0 |
FG | 20.0 |
GH | 20.0 |
IH | 17.0 |
IJ | 8.0 |
JK | 4.0 |
