��Ŀ����
����Ŀ���þ���ķ�������������еĻҳ�����Ҫ�����跨ʹ�����еĻҳ�����һ���ĵ�ɣ�Ȼ�����þ��糡�Ե�ɵ���������ʹ�ҳ��˶���ָ������������ռ���Ϊ���㣬����Ϊÿ���ҳ����������������������������ͬ����ÿ���ҳ����������Ϊq�������ܿ������������ٶȴ�С�����ȣ�����ʽΪF��=kv��ʽ��kΪ����0����֪�����������ڻҳ�������������С��Ϊ���㣬�ҳ������ڿ������ܵ糡�����ú�ﵽ�糡�������������ȵĹ������õ�ʱ�估ͨ����λ�ƾ��ɺ��Բ��ƣ�ͬʱҲ���ƻҳ�����֮������������ҳ�����������Ӱ�졣

��1����һ�־����������Ʒ����������ģ���Ҫ�����Ŀռ���һ����ΪH����ԵԲͰ���������ڲ�����һ����ԲͰ�뾶��ȵ�Բ����������ƽ������ԲͰ���ϡ������ˣ�ǡ���ܽ�ԲͰ��գ���ͼ10����ʾ����ԲͰ�ϡ��������������Ϻ㶨�ĵ�ѹU��ԲͰ�ڿռ�ĵ糡����Ϊ��ǿ�糡�����������һ��ʱ���ڽ�ԲͰ�����ڵĴ���ҳ�������ȫ�����ڽ������ϣ��Ӷ��ﵽ���������á���ҳ������˶��ɴﵽ��������� __________��
��2������һ���������İ뾶ΪR����ԵԲͰ�������ڲ��������������һ�־�������ķ�������ԲͰ��������һ��ϸֱ������Ϊ�缫������ԲͰ�ڱڼ�һ��������Ͱ��Ϊ��һ�缫����ֱ���ߵ缫��������һ���ɾ�Ե�����Ƴɵ��뾶ΪR0��ԲͰ�������ܣ���������ֱ�����غϣ���ͼ10����ʾ���������缫����Ϻ㶨�ĵ�ѹ��ʹ��Ͱ�ڴ��糡ǿ���Ĵ�Сǡ�õ��ڵڣ�1���ʵķ�����ԲͰ�ڵ糡ǿ�ȵĴ�С������֪�˷�������ԲͰ�뾶����糡ǿ�ȴ�СE�ķֲ����ΪE��1/r��ʽ��rΪ���о��ĵ���ֱ���ߵľ��롣
����ͨ���������������ҳ�����������������˶���ԲͰ�ڱ��Ĺ����У���˲ʱ�ٶȴ�Сv������ֱ���ߵľ���r֮��Ĺ�ϵ________��
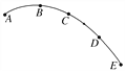
������ֱ���˶����̿����н�������v - tͼ�����������λ�Ƶķ������������˷���������v��r�仯�Ĺ�ϵ������1/v��r�仯��ͼ����ͼ�������������ҳ�����������������˶���ԲͰ�ڱ���ʱ��____________��
���𰸡� ![]()
![]()
![]()
����������1��ԲͰ�������ڵĵ糡ǿ��![]() �ҳ��������ܵĵ糡����С
�ҳ��������ܵĵ糡����С ![]() ��
��
�糡����������������ƽ��ʱ���ҳ��ﵽ������ٶȣ�����Ϊv1��
����![]()
��� ![]()
��2�������ڻҳ��������ڴ��ĵ糡ǿ��������ֱ���߾�����������С����Ͱ�ڴ��ĵ糡ǿ��Ϊ�ڣ�1���ʷ����г�ǿ�Ĵ�СE1=U/H�����ھ�ֱ����Ϊr���ij�ǿ��СΪE2��
��![]() �����E2=
�����E2=![]()
����ֱ����Խ�������糡ǿ��Խ����ҳ������˶�����ֱ���߾���Ϊrʱ���ٶ�Ϊv���� kv=qE2
���![]()
��ʽ�������ҳ�������ԲͰ�ڱ��˶������У��ٶ�����С�ġ�
����rΪ���ᣬ��1/vΪ���ᣬ����1/v-r��ͼ����ͼ��ʾ��
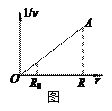
��r��r+��rС�����ڣ��糡ǿ�ȿ���Ϊ��ͬ�����ٶ�v����Ϊ��ͬ����Ӧ�ڦ�r��һ��1/v-r��ͼ���µ����Ϊ![]() ����Ȼ�����С���ε�������ڻҳ���ͨ����r��ʱ��
����Ȼ�����С���ε�������ڻҳ���ͨ����r��ʱ��![]() �����ԣ��ҳ����ӱ���������˶���ԲͰ�ڱ��������ʱ��t2���ڴ�R0��Rһ��1/v-r��ͼ���µ������
�����ԣ��ҳ����ӱ���������˶���ԲͰ�ڱ��������ʱ��t2���ڴ�R0��Rһ��1/v-r��ͼ���µ������
���Իҳ������ӱ���������˶���ԲͰ�ڱڵ�ʱ����![]()

 ȫ�Ų��Ծ�ϵ�д�
ȫ�Ų��Ծ�ϵ�д� ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�