��Ŀ����
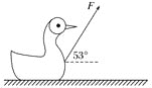
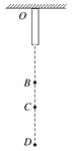
����Ŀ����ͼ��ʾ��ˮƽ��������һ���ӣ�����ֱ����Ϊ��Բ��OΪԲ�ģ���ABΪ��ˮƽ�����ֱ����Բ������һ��C���ҡ�COD=60��������A���Գ��ٶ�v1��AB����ƽ��һС��С���пӱ��ϵ���͵�D������C���Գ��ٶ�v2��BA����ƽ��С��Ҳ�ܻ���D�㣮�������ٶ�Ϊg������˵����ȷ���ǣ�������

A. �׳�ʱ��������ٶȴ�С֮��Ϊv1��v2=2��![]()
B. �׳�ʱ��������ٶȴ�С֮��Ϊv1��v2=![]() ��3
��3
C. �˶���D��ʱ��������ٶȷ���ļн�Ϊ60��
D. ������ͬʱ�׳����ٶȴ�С���ʣ�����������ڿ�������
���𰸡�B
��������С������ֱ���������������˶�����![]() ����ã�
����ã� ![]() �������½��ĸ߶�֮��Ϊh1��h2=2��1�����˶���ʱ��֮��Ϊt1��t2=
�������½��ĸ߶�֮��Ϊh1��h2=2��1�����˶���ʱ��֮��Ϊt1��t2= ![]() ��1���ɼ��ι�ϵ֪�������ˮƽλ��֮��Ϊx1��x2=2��
��1���ɼ��ι�ϵ֪�������ˮƽλ��֮��Ϊx1��x2=2��![]() ���ɹ�ʽx=v0t�ɵ�����ij��ٶ�֮��Ϊv1��v2=
���ɹ�ʽx=v0t�ɵ�����ij��ٶ�֮��Ϊv1��v2= ![]() ��3����A����B��ȷ�������������䵽D��ʱ��ˮƽ����ļнǷֱ�Ϊ����������
��3����A����B��ȷ�������������䵽D��ʱ��ˮƽ����ļнǷֱ�Ϊ����������![]() ��
�� ![]() ���ɵ�tan��=
���ɵ�tan��= ![]() tan����������ѧ֪ʶ�ɵ�֪��+����120���������˶���D��ʱ��������ٶȷ���ļнDz�����60������C������������ͬʱ�׳������ڸ߶Ⱦ���С���ڿ����˶���ʱ�䣬�������С����˶���D�㣬�����ڿ��в�������������D��������B��ȷ��ACD����
tan����������ѧ֪ʶ�ɵ�֪��+����120���������˶���D��ʱ��������ٶȷ���ļнDz�����60������C������������ͬʱ�׳������ڸ߶Ⱦ���С���ڿ����˶���ʱ�䣬�������С����˶���D�㣬�����ڿ��в�������������D��������B��ȷ��ACD����