题目内容
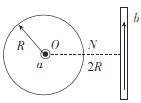
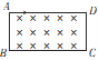
【题目】如图所示，在矩形区域(含边界)存在垂直纸面向里的匀强磁场，磁感应强度大小B0=2.0×10-2T，A、B、C、D为矩形的四个顶点，BC边长l1=4m，AB边长l2=2m。大量质量m=3.2×10-26kg、带电荷量q=-1.6×10-18C的粒子，从A点沿AD方向以不同的速率射入匀强磁场中，粒子恰好均从BC边射出，不计粒子重力及粒子间的作用力。求：
（1）粒子的速率的取值范围；
（2）粒子在磁场中运动的最长时间。
【答案】（1）
；（2）
【解析】
(1)粒子恰好均从BC边射出，可知粒子以最小速率v1运动时恰好打在B点，由几何关系可知其半径
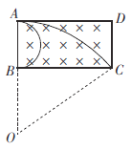
可知粒子以最大速率v2运动时恰好打在C点，设其半径为R2，由几何关系
解得
m
粒子在匀强磁场中运动，由洛伦兹力提供向心力，有
可得
解得
则粒子的速率的取值范围为
(2)从B点射出的粒子在磁场中运动的时间最长，其运动时间
而
解得
s
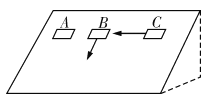
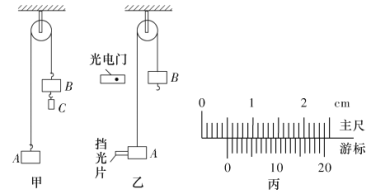
课课通课程标准思维方法与能力训练系列答案【题目】某同学利用下述装置对轻质弹簧的弹性势能进行探究，一轻质弹簧放置在光滑水平桌面上，弹簧左端固定，右端与一小球接触而不固连:弹簧处于原长时，小球恰好在桌面边缘，如图（a）所示。向左推小球，使弹簧压缩一段距离后由静止释放。小球离开桌面后落到水平地面。通过测量和计算，可求得弹簧被压缩后的弹性势能。
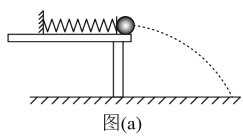
回答下列问题：
（1）本实验中可认为，弹簧被压缩后的弹性势能Ep与小球抛出时的动能Ek相等。已知重力加速度大小为g，为求得Ek，至少需要测量下列物理量中的 （填正确答案标号）。
A．小球的质量m |
B．小球抛出点到落地点的水平距离s |
C．桌面到地面的高度h |
D．弹簧的压缩量△x |
E.弹簧原长l0
（2）用所选取的测量量和已知量表示Ek，得Ek= 。
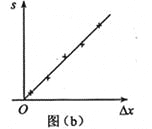
（3）图（b）中的直线是实验测量得到的s—△x图线。从理论上可推出，如果h不变。m增加，s—△x图线的斜率会 （填“增大”、“减小”或“不变”）；如果m不变，h增加，s—△x图线的斜率会 （填“增大”、“减小”或“不变”）。由图（b）中给出的直线关系和Ek的表达式可知，Ep与△x的 次方成正比。
