题目内容
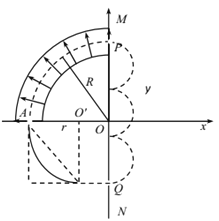
【题目】如图所示,直角坐标系xoy平面内,有一绝缘薄板MN垂直于x轴放置在x=0处,在P、Q两处分别有一小孔,OP=a,OQ=b,(a>b),在第二象限内有如图的辐向分布电场,图中A点处在以O为圆心、半径为a的圆弧上(如虚线所示),场强大小为E;在紧靠A孔处的一加速电场;在x>0区域有垂直于纸面向里的匀强磁场(未画出)。现通过加速电场将比荷为![]() 带电粒子由静止加速后从A点平行y方向进入电场,不计粒子重力,此粒子恰好能沿虚线圆弧轨迹从P点射出进入右方磁场。
带电粒子由静止加速后从A点平行y方向进入电场,不计粒子重力,此粒子恰好能沿虚线圆弧轨迹从P点射出进入右方磁场。

(1)求此加速电压U;
(2)设粒子与绝缘薄板碰撞时无电量损失且能以原速弹回,粒子刚好能穿过Q孔,求此区域的磁感应强度B1;
(3)在(2)问相同条件下,设忽略加速电场所占空间大小,若在第三象限的某区域存在另一个三角形匀强磁场区域,从Q孔射出的粒子,进入此磁场后,又恰好能垂直于x轴回到A孔,求粒子轨道半径最大时磁场的最小面积以及此磁场与第一象限磁场磁感应强度之比。
【答案】(1)![]() (2)
(2)![]()
![]()
【解析】(1)粒子经加速电场后速度为v,
由动能定理得: ![]()
粒子进入辐向磁场区城做匀速圆周运动,由牛倾第二定律有: ![]()
得: ![]()
![]()
(2)粒子垂直于y轴进入磁场,从Q点射出,则作圆周运动如图所示:
半径![]() (n=1,2,3…)
(n=1,2,3…)
由![]()
解得![]() (n=1,2,3…)
(n=1,2,3…)
(3)由几何知识知,粒子进入第三象限,作圆周运动半径r=b
所以由图示三角形区域的最小面积![]()
由牛顿第二定律得: ![]()
![]() (n=1,2,3…)
(n=1,2,3…)

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目