题目内容
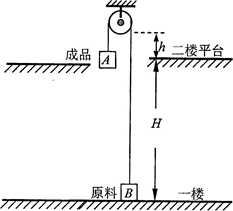
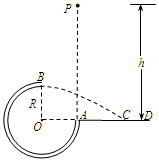
(18分)、如图所示,固定的光滑平台左端固定有一光滑的半圆轨道,轨道半径为R,平台上静止放着两个滑块A、B,其质量mA=m,mB=2m,两滑块间夹有少量炸药。平台右侧有一小车,静止在光滑的水平地面上,小车质量M=3m,车长L=2R,车面与平台的台面等高,车面粗糙,动摩擦因数μ="0.2" ,右侧地面上有一立桩,立桩与小车右端的距离为S,S在0<S<2R的范围内取值,当小车运动到立桩处立即被牢固粘连。点燃炸药后,滑块A恰好能够通过半圆轨道的最高点D,滑块B冲上小车。两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个滑块的速度方向在同一水平直线上,重力加速度为g=10m/s2。求: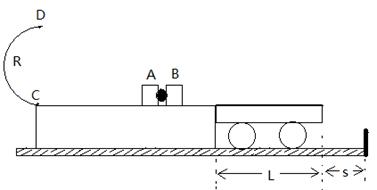
(1)滑块A在半圆轨道最低点C受到轨道的支持力FN。
(2)炸药爆炸后滑块B的速度大小VB。
(3)请讨论滑块B从滑上小车在小车上运动的过程中,克服摩擦力做的功Wf与S的关系。
(1)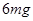 (2)
(2)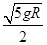 (3) 11mR
(3) 11mR
解析试题分析:(1)、以水平向右为正方向,设爆炸后滑块A的速度大小为VA,
滑块A在半圆轨道运动,设到达最高点的速度为VAD,则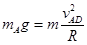 1分
1分
得到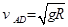 1分
1分
滑块A在半圆轨道运动过程中,
据动能定理: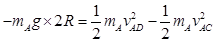 1分
1分
得:
滑块A在半圆轨道最低点: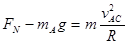 1分
1分
得: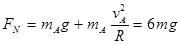 1分
1分
(2)、在A、B爆炸过程,动量守恒。则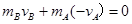 1分
1分
得: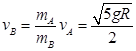 1分
1分
(3)、滑块B滑上小车直到与小车共速,设为
整个过程中,动量守恒: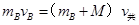 1分
1分
得: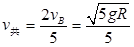 1分
1分
滑块B从滑上小车到共速时的位移为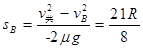 1分
1分
小车从开始运动到共速时的位移为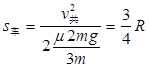 1分
1分
两者位移之差(即滑块B相对小车的位移)为: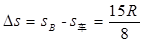 <2R,
<2R,
即滑块B与小车在达到共速时未掉下小车。 1分
当小车与立桩碰撞后小车停止,然后滑块B以V共 向右做匀减速直线运动,则直到停下来发生的位移为 S'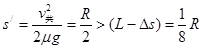 所以,滑块B会从小车滑离。1分
所以,滑块B会从小车滑离。1分
讨论:当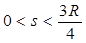 时,滑块B克服摩擦力做功为
时,滑块B克服摩擦力做功为 1分
1分
当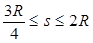
 时,滑块B从滑上小车到共速时克服摩擦力做功为
时,滑块B从滑上小车到共速时克服摩擦力做功为 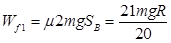 1分
1分
然后滑块B以Vt向右做匀减速直线运动,则直到停下来发生的位移为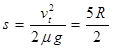 >2R 所以,滑块会从小车滑离。 1分
>2R 所以,滑块会从小车滑离。 1分
则滑块共速后在小车运动时克服摩擦力做功为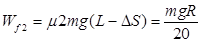 1分
1分
所以,当
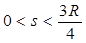 时,滑块B克服摩擦力做功为
时,滑块B克服摩擦力做功为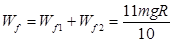 ="11mR" 1分
="11mR" 1分
考点: 牛顿第二定律 动能定理 动量守恒 功

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案 。质量为2.0kg的金属杆ab垂直导轨放置,其他电阻不计。用恒力沿导轨平面向下拉金属杆ab,由静止开始运动,8s末杆运动刚好达到最大速度为8m/s,这8s内金属杆的位移为48m,(g=10m/s2,cos370=0.8,sin370=0.6)
。质量为2.0kg的金属杆ab垂直导轨放置,其他电阻不计。用恒力沿导轨平面向下拉金属杆ab,由静止开始运动,8s末杆运动刚好达到最大速度为8m/s,这8s内金属杆的位移为48m,(g=10m/s2,cos370=0.8,sin370=0.6)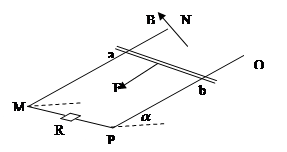


 ,其他电阻不计。导轨间距为d=0.8m,矩形区域MNPQ内存在有界匀强磁场,场强大小B=0.25T。MN=PQ=x=0.85m,金属棒与两导轨间动摩擦因数都为0.4,电阻R与边界MP的距离s=0.36m。在外力作用下让ab棒由静止开始匀加速运动并穿过磁场向右,加速度a=2m/s2 ,g取10m/s2
,其他电阻不计。导轨间距为d=0.8m,矩形区域MNPQ内存在有界匀强磁场,场强大小B=0.25T。MN=PQ=x=0.85m,金属棒与两导轨间动摩擦因数都为0.4,电阻R与边界MP的距离s=0.36m。在外力作用下让ab棒由静止开始匀加速运动并穿过磁场向右,加速度a=2m/s2 ,g取10m/s2