题目内容
10．
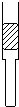如图所示，一根上粗下细（上下两段各自粗细均匀）的玻璃管上端开口、下端封闭，上端足够长，下端有一段水银柱封闭了一定质量的理想气体．现将封闭气体温度同时缓慢降低，在气体温度不断下降过程中，水银柱缓慢向下移动，则下图中的图线最接近被封闭气体体积V和热力学温度T关系的是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 气体温度不断升高，水银柱上升，当水银柱未进入细管时，封闭气体压强不变，发生等压变化，根据盖-吕萨克定律，体积与热力学温度成正比．当水银柱进入细管时，封闭气体的压强逐渐增大．当水银柱完全进入粗管时，封闭气体又等压变化．本题根据盖-吕萨克定律和气态方程研究．
解答 解：当水银柱未进入细管时，封闭气体压强不变，发生等压变化，根据盖-吕萨克定律，体积与热力学温度成正比，V-t图象是过原点的倾斜的直线．
当水银柱进入细管时，封闭气体的压强逐渐减小，由题可知，T增大，V增大，
由气态方程$\frac{PV}{T}=C$，得：$\frac{V}{T}=\frac{C}{P}$，
图线上的点与原点连线的斜率K=$\frac{V}{T}$，当P减小时，K增大．
当水银柱完全进入粗管时，封闭气体压强不变，发生等压变化，根据盖-吕萨克定律，体积与热力学温度成正比，$\frac{V}{T}$=c′=$\frac{C}{P′}$，V-t图象也是过原点的倾斜的直线，因为P＞P′则这段直线斜率增大．
故选：A．
点评 本题考查分析理解物理图象的能力．本题也可以就根据气态方程研究．关键要抓住水银未进入粗管和完全进入过程，封闭气体发生等压变化．
练习册系列答案
相关题目
20．下列关于速度和加速度的说法中，正确的是（ ）
| A． | 物体运动的速度改变越大，它的加速度一定越大 | |
| B． | 物体运动的加速度为零，它的速度也一定为零 | |
| C． | 物体运动的速度改变越小，它的加速度一定越小 | |
| D． | 加速度的大小是表示物体运动速度变化率的大小 |
1．
如图所示，在光滑水平面上放一木板；木板的左端放一物体，对物体施加一水平恒力F，将物体由静止开始直到从木板右端拉出．如果第一次木板被固定在地面上，第二次木板未被固定，则这两种情况下（ ）
如图所示，在光滑水平面上放一木板；木板的左端放一物体，对物体施加一水平恒力F，将物体由静止开始直到从木板右端拉出．如果第一次木板被固定在地面上，第二次木板未被固定，则这两种情况下（ ）| A． | 摩擦力大小相同 | B． | F做的功相同 | ||
| C． | 摩擦产生的热相同 | D． | 物体获得的动能相同 |
18．
如图所示，电阻为R，其他电阻均可忽略，ef是一电阻不计的水平放置的导体棒，质量为m，棒的两端分别与ab、cd保持良好的接触，又能沿框架无摩擦下滑，整个装置放在与框架垂直的匀强磁场中，当ef从静止下滑经一段时间后闭合S，则S闭合后（ ）
如图所示，电阻为R，其他电阻均可忽略，ef是一电阻不计的水平放置的导体棒，质量为m，棒的两端分别与ab、cd保持良好的接触，又能沿框架无摩擦下滑，整个装置放在与框架垂直的匀强磁场中，当ef从静止下滑经一段时间后闭合S，则S闭合后（ ）| A． | ef的加速度可能大于g | |
| B． | ef的加速度一定小于g | |
| C． | ef最终速度随S闭合时刻的不同而不同 | |
| D． | ef的机械能与回路内产生的电能之和一定不变 |
5．在《探究加速度与力、质量的关系》实验中，某同学在某次实验时释放小车的瞬间装置状态如图1．
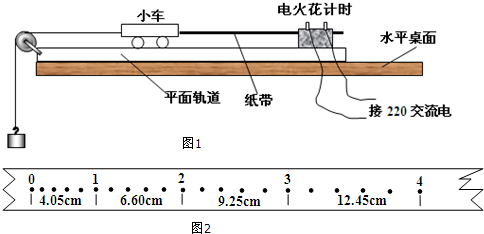
（Ⅰ）则操作中有待改进的是：①小车离计时器太远；②需平衡摩擦力
（Ⅱ）如图2为改进实验操作后某次实验打下的纸带数据，相邻两计数点间距如图所示，则该次实验加速度为2.76m/s2（保留3位有效数字）
（Ⅲ）若均使用同一规格钩码以改变小车总质量和悬挂重物的总重力，某同学得到多次运动中对应加速度，实验数据如表格所示
请选择一组数据用来研究加速度与力关系，并在答题卡坐标纸上作出相应图线．
作图要求：（1）完善坐标物理量及合理的物理量标度
（2）在坐标纸上标出所选数据，完成图线并标出数据坐标值；
（3）就你所选实验数据得到的结论做出评价．
（Ⅰ）则操作中有待改进的是：①小车离计时器太远；②需平衡摩擦力
（Ⅱ）如图2为改进实验操作后某次实验打下的纸带数据，相邻两计数点间距如图所示，则该次实验加速度为2.76m/s2（保留3位有效数字）
（Ⅲ）若均使用同一规格钩码以改变小车总质量和悬挂重物的总重力，某同学得到多次运动中对应加速度，实验数据如表格所示
| 小车钩码数 最悬挂钩码数 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1.39m/s2 | 1.16m/s2 | 1.00m/s2 | 0.94m/s2 | 0.78m/s2 |
| 2 | 2.48m/s2 | 2.20m/s2 | 2.00m/s2 | 1.81m/s2 | / |
| 3 | 3.38m/s2 | 2.89m/s2 | 2.76m/s2 | / | / |
| 4 | 4.15m/s2 | 3.68m/s2 | / | / | / |
| 5 | 4.59m/s2 | / | / | / | / |
作图要求：（1）完善坐标物理量及合理的物理量标度
（2）在坐标纸上标出所选数据，完成图线并标出数据坐标值；
（3）就你所选实验数据得到的结论做出评价．
15．两个球形行星A和B各有一颗靠近表面的卫星a和b．若这两颗卫星的周期之比Ta：Tb=p，半径之比RA：RB=q，则此两个行星的质量之比MA：MB为（ ）
| A． | $\frac{q}{p}$ | B． | $\sqrt{\frac{q}{p}}$ | C． | $\frac{{q}^{2}}{{p}^{3}}$ | D． | $\frac{{q}^{3}}{{p}^{2}}$ |
如图所示，A、B两物体通过一柔软且不可以伸长的软绳连接，跨在光滑小滑轮两侧，软绳与水瓶接触面平行，已知A、B两物体的质量为m，且可视为质点，软绳质量也为m，长为2L，平台离地面高围殴L，不计运动过程中的一切摩擦．初软绳全部在水平面内，现无初速释放B，A、B在重力作用下开始运动，若B触地后不再反弹．
19．
1913年美国物理学家密立根设计了著名的油滴实验，首先直接测定了基元电荷的量值．其模型简化如图，平行板电容器两极板M、N相距d，两极板分别与电压为U的恒定电源两极连接，极板M带正电．现有一质量为m的带电油滴在极板中央处于静止状态，且此时极板带电荷量与油滴带电荷量的比值为k，则（ ）
1913年美国物理学家密立根设计了著名的油滴实验，首先直接测定了基元电荷的量值．其模型简化如图，平行板电容器两极板M、N相距d，两极板分别与电压为U的恒定电源两极连接，极板M带正电．现有一质量为m的带电油滴在极板中央处于静止状态，且此时极板带电荷量与油滴带电荷量的比值为k，则（ ）| A． | 油滴带正电 | |
| B． | 油滴带电荷量为$\frac{mg}{Ud}$ | |
| C． | 电容器的电容为$\frac{kmgd}{U^2}$ | |
| D． | 将极板N向下缓慢移动一小段距离，油滴将向上运动 |
如图所示，一个被x轴与曲线方程y=0.2sin$\frac{10π}{3}$x（m）所围的空间存在着匀强磁场．磁场方向垂直纸面向里，磁感应强度B=0.2T．正方形金属线框的边长是L=0.2m，电阻是R=0.1Ω，它的一边与x轴重合，在拉力F的作用下，以v=10m/s的速度水平向右匀速运动．求：