题目内容
15.两个球形行星A和B各有一颗靠近表面的卫星a和b.若这两颗卫星的周期之比Ta:Tb=p,半径之比RA:RB=q,则此两个行星的质量之比MA:MB为( )| A. | $\frac{q}{p}$ | B. | $\sqrt{\frac{q}{p}}$ | C. | $\frac{{q}^{2}}{{p}^{3}}$ | D. | $\frac{{q}^{3}}{{p}^{2}}$ |
分析 卫星做圆周运动,万有引力提供向心力,求出质量和周期以及运行半径R之间的关系可得.
解答 解:卫星做圆周运动时,万有引力提供圆周运动的向心力,则有:$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}R}{{T}^{2}}$
解得:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,
则$\frac{{M}_{A}}{{M}_{B}}=\frac{\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}}{\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}}=\frac{{q}^{3}}{{p}^{2}}$,故D正确.
故选:D
点评 根据万有引力提供向心力列出方程,得到质量之比和半径以及周期之间的关系,代入数据可得结论.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2m,BC=3m.且物体通过AB、BC、CD所用时间相等.
物体自O点由静止开始做匀加速直线运动,A、B、C、D为其运动轨迹上的四点,测得AB=2m,BC=3m.且物体通过AB、BC、CD所用时间相等. 如图甲所示,固定在水平面上电阻不计的光滑金属导轨,间距d=5m,导轨右端连接一阻值为R=4Ω的小灯泡L.在CDEF矩形区域内有竖直向上的匀强磁场,磁感应强度B随时间t变化如图乙所示,CF长为2m.在t=0时刻,电阻为1Ω的金属棒ab在水平恒力F作用下,由静止开始沿导轨向右运动.金属棒从图中位置运动到EF位置的整个过程中,小灯泡的亮度始终没有发生变化.求:
如图甲所示,固定在水平面上电阻不计的光滑金属导轨,间距d=5m,导轨右端连接一阻值为R=4Ω的小灯泡L.在CDEF矩形区域内有竖直向上的匀强磁场,磁感应强度B随时间t变化如图乙所示,CF长为2m.在t=0时刻,电阻为1Ω的金属棒ab在水平恒力F作用下,由静止开始沿导轨向右运动.金属棒从图中位置运动到EF位置的整个过程中,小灯泡的亮度始终没有发生变化.求: 一物体质量为2kg,在动力摩擦因数为0.05的水平面上受到水平力作用,其v-t突显如图所示,则在物体运动过程中,求水平力F所做的总功、平均功率和最大瞬间功率.(g=10m/s2)
一物体质量为2kg,在动力摩擦因数为0.05的水平面上受到水平力作用,其v-t突显如图所示,则在物体运动过程中,求水平力F所做的总功、平均功率和最大瞬间功率.(g=10m/s2)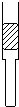 如图所示,一根上粗下细(上下两段各自粗细均匀)的玻璃管上端开口、下端封闭,上端足够长,下端有一段水银柱封闭了一定质量的理想气体.现将封闭气体温度同时缓慢降低,在气体温度不断下降过程中,水银柱缓慢向下移动,则下图中的图线最接近被封闭气体体积V和热力学温度T关系的是( )
如图所示,一根上粗下细(上下两段各自粗细均匀)的玻璃管上端开口、下端封闭,上端足够长,下端有一段水银柱封闭了一定质量的理想气体.现将封闭气体温度同时缓慢降低,在气体温度不断下降过程中,水银柱缓慢向下移动,则下图中的图线最接近被封闭气体体积V和热力学温度T关系的是( )




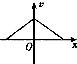
 某静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一个带负电的粒子(忽略重力)在电场中以x=0为中心、沿x轴方向做周期性运动.取x轴正方向为电场强度E、粒子加速度a、速度.的正方向,下图分别表示x轴上各点的电场强度E、粒子的加速度a.速度v和动能Ek随x的变化图象,其中可能正确的是( )
某静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线.一个带负电的粒子(忽略重力)在电场中以x=0为中心、沿x轴方向做周期性运动.取x轴正方向为电场强度E、粒子加速度a、速度.的正方向,下图分别表示x轴上各点的电场强度E、粒子的加速度a.速度v和动能Ek随x的变化图象,其中可能正确的是( )


 水平放置的导体框架,宽L=0.50m,接有电阻R=0.20Ω,匀强磁场垂直框架平面向里,磁感应强度B=0.40T.一导体棒ab垂直框边跨放在框架上,并能无摩擦地在框架上滑动,框架和导体ab的电阻均不计.当ab以v=4.0m/s的速度向右匀速滑动时,求:
水平放置的导体框架,宽L=0.50m,接有电阻R=0.20Ω,匀强磁场垂直框架平面向里,磁感应强度B=0.40T.一导体棒ab垂直框边跨放在框架上,并能无摩擦地在框架上滑动,框架和导体ab的电阻均不计.当ab以v=4.0m/s的速度向右匀速滑动时,求: