题目内容
如图所示，半径为R，内表面光滑的半球形容器放在光滑的水平面上，容器左侧靠着竖直墙壁，一个质量为m的小球，从容器顶端A无初速释放，小球能沿球面上升的最大高度距球面底部B的距离为3R/4，小球的运动在竖直平面内。求：
（1）容器的质量M
（2）竖直墙作用于容器的最大冲量。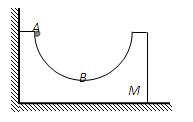
（1）容器的质量M
（2）竖直墙作用于容器的最大冲量。
（1）在A球释放到B点时，M未动，对A由机械能守恒有：
mgR=mv02（2分）
此后A继续向右
运动，但B在A给它作用力情况下，离开墙壁向右运动，
对A、B系统：由水平方向动量守恒得：
mv0="(M+m)" v1（2分）
由机械能守恒得：
mg·R=mv02－(M+m) v12（2分）
由以上三式解得v0= M=3m（2分）
（2）由于在A球释放到B点时，M未动，此后M离开墙壁向右运动，所以对A、B系统来讲，由动量定理知，竖直墙对容器的最大冲量为A球水平动量的变化，
即Im=mv0
代入v0得Im=m（2分）
mgR=mv02（2分）
此后A继续向右
运动，但B在A给它作用力情况下，离开墙壁向右运动，对A、B系统：由水平方向动量守恒得：
mv0="(M+m)" v1（2分）
由机械能守恒得：
mg·R=mv02－(M+m) v12（2分）
由以上三式解得v0= M=3m（2分）
（2）由于在A球释放到B点时，M未动，此后M离开墙壁向右运动，所以对A、B系统来讲，由动量定理知，竖直墙对容器的最大冲量为A球水平动量的变化，
即Im=mv0
代入v0得Im=m（2分）
略
练习册系列答案
相关题目
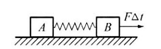
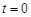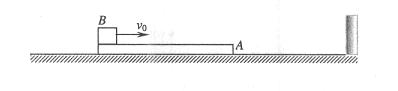
时使二者获得等大反向的初速度开始运动，经过时间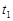
铁块在木块上停止滑动，二者相对静止，此时与开始运动的位置相比较，图中哪一幅反映了可能发生的情况（ ）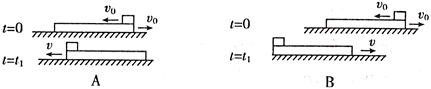
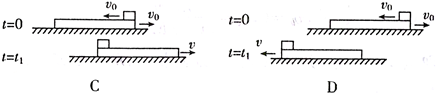
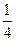圆弧槽C与长木板接触但不连接，圆弧槽的下端与木板的上表面相平，B、C静止在水平面上。现有滑块A以初速度v0从右端滑上B并以v0/2滑离B，恰好能到达C的最高点。A、B、C的质量均为m，试求 ：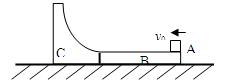
B球为s处自由释放，并与B球发生正碰。碰撞中无机械能损失，且A球的电荷量始终不变。已知B球的质量M=3m，B球被碰后作周期性运动，其运动周期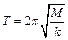
（A、B小球均可视为质点）。求：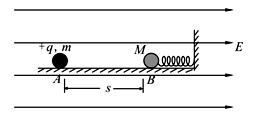
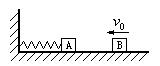
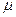。现使二者一起以初速度
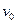开始向右运动，运动一段距离后，长木板A与固定竖直挡板相撞。已知A与挡板碰撞时间极短，且无机械能损失。运动过程中，B始终没从长木板A上脱落。求：
