题目内容
14. 如图所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°,在第Ⅲ象限垂直于桌面放置两块相互平行的绝缘平板C1和C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其靠近左端紧贴桌面有一小孔M,离坐标原点O的距离为L=0.72m,在第Ⅳ象限垂直于x轴放置一足够长绝缘平板C3,其一端位于垂足Q,Q点与原点O相距d2=0.18m,现将一带负电的小球从桌面上的P点(P点和原点O在同一电场线上),以初速度V0=2$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔进入磁场区域小球可视为质点,小球的比荷$\frac{q}{m}$=20c/kg,不考虑空气阻力和小球电荷量的变化.(结果保留两位有效数字)求:
如图所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°,在第Ⅲ象限垂直于桌面放置两块相互平行的绝缘平板C1和C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其靠近左端紧贴桌面有一小孔M,离坐标原点O的距离为L=0.72m,在第Ⅳ象限垂直于x轴放置一足够长绝缘平板C3,其一端位于垂足Q,Q点与原点O相距d2=0.18m,现将一带负电的小球从桌面上的P点(P点和原点O在同一电场线上),以初速度V0=2$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔进入磁场区域小球可视为质点,小球的比荷$\frac{q}{m}$=20c/kg,不考虑空气阻力和小球电荷量的变化.(结果保留两位有效数字)求:(1)匀强电场的场强大小;
(2)要使带电小球无碰撞地穿出磁场并打到平板C3上,求磁感应强度B的取值范围.
分析 (1)小球在第Ⅱ象限内做类平抛运动,分别写出沿电场方向和垂直于电场方向的分位移、分速度与时间的关系式,结合牛顿第二定律求出加速度,联立可得到场强的大小.
(2)根据类平抛运动的规律求出经过M点的速度,作出粒子在磁场中的临界运动轨迹,结合几何关系和半径公式求出磁感应强度的范围.
解答 解:(1)小球在第Ⅱ象限内做类平抛运动,则有
L1sinθ=v0t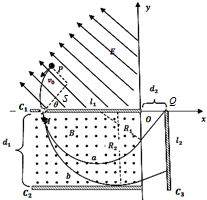
v0tanθ=at
由牛顿第二定律得 qE=ma
联立解得 E=$\frac{5}{9}$$\sqrt{2}$N/C≈0.79N/C
(2)设小球通过M点时的速度为v
由类平抛运动的规律有 v=$\frac{{v}_{0}}{sinθ}$=4m/s
小球垂直磁场方向进入两板间做匀速圆周运动,轨迹如图,由牛顿第二定律有:
qvB=m$\frac{{v}^{2}}{R}$
得:B=$\frac{mv}{qR}$
小球刚好能打到Q点磁感应强度最强,设为B1.此时小球的轨迹半径为R1,由几何关系有:$\frac{{R}_{1}}{{l}_{1}+{d}_{2}-{R}_{1}}$=$\frac{{l}_{1}-{R}_{1}}{{R}_{1}}$
代入数据解得:B1=0.5T.
小球刚好不与C2板相碰时磁感应强度最小,设为B2,此时粒子的轨迹半径为R2,由几何关系有:
R2=d1
代入数据解得:B2=$\frac{1}{3}$T≈0.33T.
综合得磁感应强度的取值范围:0.33T≤B≤0.5T
答:
(1)匀强电场的场强大小为0.79N/C;
(2)磁感应强度B的取值范围为0.33T≤B≤0.5T.
点评 本题关键是明确粒子的运动规律、画出运动轨迹,然后结合牛顿第二定律、类似平抛运动的分位移公式和几何关系列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 某制药厂的污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左、右两端开口,在垂直于上、下底面方向加磁感应强度为B,方向向下的匀强磁场,在前、后两个面的内侧固定有金属板作为电极,当含有大量正、负离子(其重力不计)的污水充满管口从左向右流经该装置时,利用电压表所显示的两个电极间的电压U,就可测出污水流量Q(单位时间内流出的污水体积).则下列说法正确的是( )
某制药厂的污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左、右两端开口,在垂直于上、下底面方向加磁感应强度为B,方向向下的匀强磁场,在前、后两个面的内侧固定有金属板作为电极,当含有大量正、负离子(其重力不计)的污水充满管口从左向右流经该装置时,利用电压表所显示的两个电极间的电压U,就可测出污水流量Q(单位时间内流出的污水体积).则下列说法正确的是( )
 某制药厂的污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左、右两端开口,在垂直于上、下底面方向加磁感应强度为B,方向向下的匀强磁场,在前、后两个面的内侧固定有金属板作为电极,当含有大量正、负离子(其重力不计)的污水充满管口从左向右流经该装置时,利用电压表所显示的两个电极间的电压U,就可测出污水流量Q(单位时间内流出的污水体积).则下列说法正确的是( )
某制药厂的污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左、右两端开口,在垂直于上、下底面方向加磁感应强度为B,方向向下的匀强磁场,在前、后两个面的内侧固定有金属板作为电极,当含有大量正、负离子(其重力不计)的污水充满管口从左向右流经该装置时,利用电压表所显示的两个电极间的电压U,就可测出污水流量Q(单位时间内流出的污水体积).则下列说法正确的是( )| A. | 后表面的电势一定高于前表面的电势,与正、负哪种离子多少无关 | |
| B. | 若污水中正、负离子数相同,则前、后表面的电势差为零 | |
| C. | 在一定范围内,流量Q越大,两个电极间的电压U越大 | |
| D. | 污水中离子数越多,两个电极间的电压U越大 |
19. 一个国际研究小组借助于智利超大望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.此双星系统中体积较小成员能“吸食”另一颗体积较大星体表面物质,达到质量转移的目的,假设在演变的过程中两者球心之间的距离保持不变,演变初期体积较大星体的质量较大,则在最初演变的过程中下列说法正确的是( )
一个国际研究小组借助于智利超大望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.此双星系统中体积较小成员能“吸食”另一颗体积较大星体表面物质,达到质量转移的目的,假设在演变的过程中两者球心之间的距离保持不变,演变初期体积较大星体的质量较大,则在最初演变的过程中下列说法正确的是( )
 一个国际研究小组借助于智利超大望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.此双星系统中体积较小成员能“吸食”另一颗体积较大星体表面物质,达到质量转移的目的,假设在演变的过程中两者球心之间的距离保持不变,演变初期体积较大星体的质量较大,则在最初演变的过程中下列说法正确的是( )
一个国际研究小组借助于智利超大望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图所示.此双星系统中体积较小成员能“吸食”另一颗体积较大星体表面物质,达到质量转移的目的,假设在演变的过程中两者球心之间的距离保持不变,演变初期体积较大星体的质量较大,则在最初演变的过程中下列说法正确的是( )| A. | 体积较大星体圆周运动轨迹半径变大,线速度也变大 | |
| B. | 体积较大星体圆周运动轨迹半径变大,线速度变小 | |
| C. | 它们做圆周运动的万有引力不断改变 | |
| D. | 它们做圆周运动的万有引力保持不变 |
6.1800年前,当众人面对大象这样的庞然大物,因为缺少有效的称量工具而束手无策的时候,曹冲想出了称量大象体重的方法,被世人所称道,下列物理学习或研究中用到的方法与“曹冲称象”的方法相同的是( )
| A. | “质点”的概念 | B. | 合力与分力的关系 | ||
| C. | “瞬时速度”的概念 | D. | 研究加速度与合力、质量的关系 |
4. 据国外媒体报道,科学家预计2017年将能发现真正类似地球的“外星人”地球,这个具有历史意义的发现会使人类重新评估所处的宇宙空间.如图所示,假若“外星人”地球具有磁性,其中虚线是磁感线,实践是宇宙射线(宇宙中一种带有相当大能量的带电粒子流),则以下说法正确的是( )
据国外媒体报道,科学家预计2017年将能发现真正类似地球的“外星人”地球,这个具有历史意义的发现会使人类重新评估所处的宇宙空间.如图所示,假若“外星人”地球具有磁性,其中虚线是磁感线,实践是宇宙射线(宇宙中一种带有相当大能量的带电粒子流),则以下说法正确的是( )
 据国外媒体报道,科学家预计2017年将能发现真正类似地球的“外星人”地球,这个具有历史意义的发现会使人类重新评估所处的宇宙空间.如图所示,假若“外星人”地球具有磁性,其中虚线是磁感线,实践是宇宙射线(宇宙中一种带有相当大能量的带电粒子流),则以下说法正确的是( )
据国外媒体报道,科学家预计2017年将能发现真正类似地球的“外星人”地球,这个具有历史意义的发现会使人类重新评估所处的宇宙空间.如图所示,假若“外星人”地球具有磁性,其中虚线是磁感线,实践是宇宙射线(宇宙中一种带有相当大能量的带电粒子流),则以下说法正确的是( )| A. | a端是行星磁场的N极,b端是行星磁场的S极 | |
| B. | 从a、b端射向行星的宇宙射线,可能在a、b端不发生偏转 | |
| C. | 图中从上往下看,此行星自身的环形电流的方向应为顺时针 | |
| D. | 图中来自宇宙射线中带正电的粒子流②将垂直纸面向里偏转 |
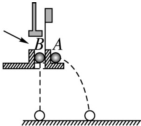 选用如图所示的装置探究平抛运动的规律时,应保持A球所在位置水平,用小锤打击弹性金属片后,两球同时开始运动,可观察到两球的落地先后情况是两球同时落地,说明A球在竖直方向做自由落体运动运动.
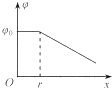
选用如图所示的装置探究平抛运动的规律时,应保持A球所在位置水平,用小锤打击弹性金属片后,两球同时开始运动,可观察到两球的落地先后情况是两球同时落地,说明A球在竖直方向做自由落体运动运动.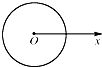 如图所示,正电荷Q均匀分布在半径为r的金属球面上.以圆心O为坐标原点,向右建立x轴,选取无穷远处电势为零,用E表示沿x轴上各点电场强度的大小、φ表示沿x轴上各点电势的高低.下列E-x和φ-x图象大致正确的是( )
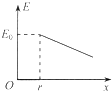
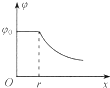
如图所示,正电荷Q均匀分布在半径为r的金属球面上.以圆心O为坐标原点,向右建立x轴,选取无穷远处电势为零,用E表示沿x轴上各点电场强度的大小、φ表示沿x轴上各点电势的高低.下列E-x和φ-x图象大致正确的是( )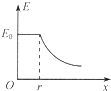
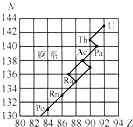 自然界里一些放射性重元素往往会发生一系列连续的衰变,形成放射系.如图是锕系图的一部分,纵坐标N表示中子数,则图中U衰变成Po,经历了5次α衰变,2次β衰变.
自然界里一些放射性重元素往往会发生一系列连续的衰变,形成放射系.如图是锕系图的一部分,纵坐标N表示中子数,则图中U衰变成Po,经历了5次α衰变,2次β衰变.