题目内容
3.同实验桌的小王与小李两同学在做用单摆测定重力加速度的实验.(1)小王同学先用20分度的游标卡尺测量摆球直径,示数如图(a)所示,则该摆球的直径d=1.415cm.
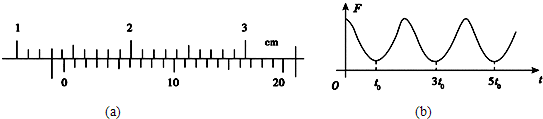
(2)接着他们测量了摆线的长度为l0,实验时用拉力传感器测得摆线的拉力F随时间t变化的图象如图(b)所示,则通过计算求重力加速度的表达式为$\frac{{π}^{2}{(2{l}_{0}+d)}^{2}}{{8{t}_{0}}^{2}}$.
(3)他们通过改变摆线长度l0,测量了多组数据,在进行数据处理时,小王同学把摆线长l0作为摆长,直接利用公式求出各组重力加速度值再求出平均值;小李同学作出T2-l0图象后求出斜率,然后算出重力加速度,两同学处理数据的方法对结果的影响是:小王偏小,小李无影响(选填“偏大”“偏小”或“无影响”).
分析 ①游标卡尺读数的方法是主尺读数加上游标读数,不需估读.
②单摆的摆长等于摆线的长度与摆球的半径之和,根据题意求出摆长.
摆球在最大位移处摆线的拉力最小,在最低点处,摆线的拉力最大,摆球从最大位移处,经最低点到达另一测最大位移处,然后再次反向通过最低点,最后回到最初的位置,经历的时间是一个周期,摆线的拉力经历三个最小值,由图乙所示图象求出单摆的周期T;最后由单摆周期公式求出重力加速度的表达式.
③根据单摆周期公式判断甲的测量值与真实值间的关系;由单摆周期公式的变形公式求出T2-L关系表达式,然后根据图象求出重力加速度,然后判断测量值与真实值间的关系
解答 解:①游标卡尺的读数=主尺+游标尺与主尺对齐的各数×精确度=14mm+3×0.05mm=14.15mm
②单摆摆长等于摆线长度与摆球半径之和,则单摆摆长为l=L0+$\frac{d}{2}$,
由图乙所示图象可知,单摆的周期T=5t0-t0=4t0,由单摆周期公式T=2π$\sqrt{\frac{l}{g}}$ 可知,
重力加速度为:g=$\frac{4{π}^{2}l}{{T}^{2}}$=$\frac{4{π}^{2}{({l}_{0}+\frac{d}{2})}^{2}}{{(4{t}_{0})}^{2}}$=$\frac{{π}^{2}{(2{l}_{0}+d)}^{2}}{{8{t}_{0}}^{2}}$.
③由单摆周期公式T=2π$\sqrt{\frac{l}{g}}$ 可知,重力加速度g=$\frac{4{π}^{2}l}{{T}^{2}}$
摆长应该是摆线长度与摆球半径之和,
甲同学把摆线长L作为摆长,摆长小于实际摆长,由g=$\frac{4{π}^{2}l}{{T}^{2}}$
可知,重力加速度的测量值小于真实值;
由T=2π$\sqrt{\frac{l}{g}}$ 可知,L=$\frac{g{T}^{2}}{4{π}^{2}}$=kT2,其中k=$\frac{g}{4{π}^{2}}$,由此可见,L与T2成正比,k是比例常数;
由于单摆摆长偏大还是偏小不影响图象的斜率k,因此摆长偏小不影响重力加速度的测量值.
故答案为:(1)1.415 cm (2)$\frac{{π}^{2}{(2{l}_{0}+d)}^{2}}{{8{t}_{0}}^{2}}$ (3)偏小 无影响
点评 根据图乙所示图象求出单摆的周期是易错点,要掌握单摆的运动过程,结合图象求出单摆周期;熟练应用单摆周期公式是正确解题的关键

 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案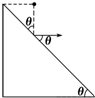 如图所示为一长为$\sqrt{2}$L、倾角θ=45°的固定斜面.今有一弹性小球,自与斜面上端等高的某处自由释放,小球落到斜面上反弹时,速度大小不变,碰撞前后,速度方向与斜面夹角相等,若不计空气阻力,欲使小球恰好落到斜面下端,则小球释放点距斜面上端的水平距离为( )
如图所示为一长为$\sqrt{2}$L、倾角θ=45°的固定斜面.今有一弹性小球,自与斜面上端等高的某处自由释放,小球落到斜面上反弹时,速度大小不变,碰撞前后,速度方向与斜面夹角相等,若不计空气阻力,欲使小球恰好落到斜面下端,则小球释放点距斜面上端的水平距离为( )| A. | $\frac{\sqrt{2}}{4}$L | B. | $\frac{1}{4}$L | C. | $\frac{\sqrt{2}}{5}$L | D. | $\frac{1}{5}$L |
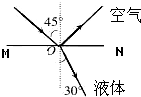 如图所示,是一束红光由空气射到某液体分界面的光路图. 当入射角是45°时,折射角为30°.下列说法正确的是( )
如图所示,是一束红光由空气射到某液体分界面的光路图. 当入射角是45°时,折射角为30°.下列说法正确的是( )| A. | 该液体对红光的折射率为$\frac{\sqrt{2}}{2}$ | |
| B. | 该液体对红光的全反射临界角为45° | |
| C. | 红光在空气和液体中的频率之比为$\sqrt{2}$:1 | |
| D. | 当紫光以同样的入射角从空气射到分界面,折射角也是30° |
| A. | $\frac{3a}{2πGR}$ | B. | $\frac{3a}{4πGR}$ | C. | $\frac{3b}{2πGR}$ | D. | $\frac{3b}{4πGR}$ |
| A. | 卡文迪许用扭秤实验测出了静电力常量 | |
| B. | 电场是人们为了了解电荷间相互作用而引入的一种并不真实存在的物质 | |
| C. | 用紫外线照射时大额钞票上用荧光物质印刷的文字会发出可见光 | |
| D. | 狭义相对论认为高速运动的物体质量会变小,运动方向的长度会变短 |
| A. | 氡的半衰期为3.8天,若取4个氡原子核,经7.6天后就一定剩下一个氡原子核了 | |
| B. | γ射线一般伴随着α或β射线产生,在这三种射线中,γ射线的穿透能力最强,电离能力最弱 | |
| C. | β衰变所释放的电子是原子核内的中子转变为质子时所产生的 | |
| D. | 若使放射性物质的温度升高,其半衰期将减小 | |
| E. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过8次α衰变和6次β衰变 |
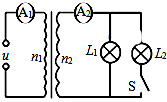 如图所示,理想变压器的输入端接交流电压,输出端并联两只相同的小灯泡L1、L2,灯泡的额定电压为20V,额定功率为10W,电路连接了两只理想电流表A1、A2,导线电阻不计.开始时电键S断开,小灯泡L1恰好正常发光.下列说法正确的是( )
如图所示,理想变压器的输入端接交流电压,输出端并联两只相同的小灯泡L1、L2,灯泡的额定电压为20V,额定功率为10W,电路连接了两只理想电流表A1、A2,导线电阻不计.开始时电键S断开,小灯泡L1恰好正常发光.下列说法正确的是( )| A. | 原副线圈的匝数比为n1:n2=3$\sqrt{2}$:1 | |
| B. | 流过小灯泡L1的电流方向每秒改变10次 | |
| C. | 电键S闭合后,小灯泡L1变暗 | |
| D. | 电键S闭合后,电流表A1的读数变大 |
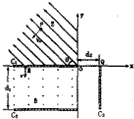 如图所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°,在第Ⅲ象限垂直于桌面放置两块相互平行的绝缘平板C1和C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其靠近左端紧贴桌面有一小孔M,离坐标原点O的距离为L=0.72m,在第Ⅳ象限垂直于x轴放置一足够长绝缘平板C3,其一端位于垂足Q,Q点与原点O相距d2=0.18m,现将一带负电的小球从桌面上的P点(P点和原点O在同一电场线上),以初速度V0=2$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔进入磁场区域小球可视为质点,小球的比荷$\frac{q}{m}$=20c/kg,不考虑空气阻力和小球电荷量的变化.(结果保留两位有效数字)求:
如图所示,在光滑绝缘水平桌面内建立xoy坐标系,在第Ⅱ象限内有平行于桌面的匀强电场,场强方向与x轴负方向的夹角θ=45°,在第Ⅲ象限垂直于桌面放置两块相互平行的绝缘平板C1和C2,两板间距为d1=0.6m,板间有竖直向上的匀强磁场,两板右端在y轴上,板C1与x轴重合,在其靠近左端紧贴桌面有一小孔M,离坐标原点O的距离为L=0.72m,在第Ⅳ象限垂直于x轴放置一足够长绝缘平板C3,其一端位于垂足Q,Q点与原点O相距d2=0.18m,现将一带负电的小球从桌面上的P点(P点和原点O在同一电场线上),以初速度V0=2$\sqrt{2}$m/s垂直于电场方向射出,刚好垂直于x轴穿过C1板上的M孔进入磁场区域小球可视为质点,小球的比荷$\frac{q}{m}$=20c/kg,不考虑空气阻力和小球电荷量的变化.(结果保留两位有效数字)求: