��Ŀ����
19�� һ�������о�С�����������������Զ�����۲��һ��˫��ϵͳ�����������������ϵ�ij��O������Բ���˶�����ͼ��ʾ����˫��ϵͳ�������С��Ա�ܡ���ʳ����һ������ϴ�����������ʣ��ﵽ����ת�Ƶ�Ŀ�ģ��������ݱ�Ĺ�������������֮��ľ��뱣�ֲ��䣬�ݱ��������ϴ�����������ϴ���������ݱ�Ĺ���������˵����ȷ���ǣ�������
һ�������о�С�����������������Զ�����۲��һ��˫��ϵͳ�����������������ϵ�ij��O������Բ���˶�����ͼ��ʾ����˫��ϵͳ�������С��Ա�ܡ���ʳ����һ������ϴ�����������ʣ��ﵽ����ת�Ƶ�Ŀ�ģ��������ݱ�Ĺ�������������֮��ľ��뱣�ֲ��䣬�ݱ��������ϴ�����������ϴ���������ݱ�Ĺ���������˵����ȷ���ǣ�������| A�� | ����ϴ�����Բ���˶��켣�뾶������ٶ�Ҳ��� | |
| B�� | ����ϴ�����Բ���˶��켣�뾶������ٶȱ�С | |
| C�� | ������Բ���˶��������������ϸı� | |
| D�� | ������Բ���˶��������������ֲ��� |
���� ˫�����������ߵ�һ��������Բ���˶������֮�����������ṩ�����������������������ɡ�ţ�ٵڶ����ɺ����������з�����
��� �⣺AB���������С����������Ϊm1������뾶Ϊr1����������������Ϊm2������뾶Ϊr2��˫�Ǽ�ľ���ΪL��ת�Ƶ�����Ϊ��m��
��m1��G$\frac{��{m}_{1}+��m����{m}_{2}-��m��}{{L}^{2}}$=��m1+��m����2r1 ��
��m2��G$\frac{��{m}_{1}+��m����{m}_{2}-��m��}{{L}^{2}}$=��m2-��m����2r2 ��
�ɢ٢ڵã���=$\sqrt{\frac{G��{m}_{1}+{m}_{2}��}{{L}^{3}}}$��������m1+m2���䣬���߾���L���䣬����ٶȦز��䣻
$\frac{{r}_{1}}{{r}_{2}}=\frac{{m}_{2}-��m}{{m}_{1}+��m}$
r1+r2=L
�����š�m�����ӣ�����ϴ������������С����ת���뾶���ӣ�����v=r�أ����ٶ����ӣ�
��A��ȷ��B����
CD�����������������һ�����������������ʱ����������������ij˻����������Բ���˶����������������ӵģ���C��ȷ��D����
��ѡ��AC
���� ������˫�����⣬Ҫץס˫��ϵͳ�����������ٶ���������ͬ������ţ�ٵڶ����ɲ��ø��뷨�����о���

| A�� | ţ�ٵ�һ���� | B�� | ţ�ٵڶ����� | C�� | ţ�ٵ������� | D�� | ������������ |
 һ�м�г�Შ�ڵ��Խ�������x������������Դλ������ԭ��O��t=0ʱ��ʼ��3sʱֹͣ��3.5sʱ�IJ�����ͼ��ʾ�������ʵ�a��ƽ��λ����O�ľ���Ϊ5.0m������˵����ȷ���ǣ�������
һ�м�г�Შ�ڵ��Խ�������x������������Դλ������ԭ��O��t=0ʱ��ʼ��3sʱֹͣ��3.5sʱ�IJ�����ͼ��ʾ�������ʵ�a��ƽ��λ����O�ľ���Ϊ5.0m������˵����ȷ���ǣ�������| A�� | ����Ϊ4m/s | |
| B�� | ����Ϊ6m | |
| C�� | ��Դ��������y�������� | |
| D�� | 2.0s��3.0s���ʵ�a��y�Ḻ�����˶� | |
| E�� | 0��3.0s���ʵ�aͨ������·��Ϊ1.4m |
| A�� | $\frac{3a}{2��GR}$ | B�� | $\frac{3a}{4��GR}$ | C�� | $\frac{3b}{2��GR}$ | D�� | $\frac{3b}{4��GR}$ |
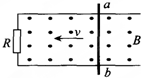 ��ͼ��ʾ���⻬�Ľ���������ڴŸ�Ӧǿ��B=0.2T����ǿ�ų��У�ƽ�е���Ŀ���d=0.3m����ֵ����R=0.5����������F�����£������ab��v=20m/s���ٶ����ŵ������������˶���������͵���ĵ��費�ƣ���
��ͼ��ʾ���⻬�Ľ���������ڴŸ�Ӧǿ��B=0.2T����ǿ�ų��У�ƽ�е���Ŀ���d=0.3m����ֵ����R=0.5����������F�����£������ab��v=20m/s���ٶ����ŵ������������˶���������͵���ĵ��費�ƣ���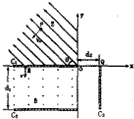 ��ͼ��ʾ���ڹ⻬��Եˮƽ�����ڽ���xoy����ϵ���ڵڢ���������ƽ�����������ǿ�糡����ǿ������x�Ḻ����ļнǦ�=45�㣬�ڵڢ�����ֱ��������������ƽ�еľ�Եƽ��C1��C2��������Ϊd1=0.6m���������ֱ���ϵ���ǿ�ų��������Ҷ���y���ϣ���C1��x���غϣ����俿����˽���������һС��M��������ԭ��O�ľ���ΪL=0.72m���ڵڢ�����ֱ��x�����һ�㹻����Եƽ��C3����һ��λ�ڴ���Q��Q����ԭ��O���d2=0.18m���ֽ�һ�������С��������ϵ�P�㣨P���ԭ��O��ͬһ�糡���ϣ����Գ��ٶ�V0=2$\sqrt{2}$m/s��ֱ�ڵ糡����������պô�ֱ��x�ᴩ��C1���ϵ�M����ų�����С�����Ϊ�ʵ㣬С��ıȺ�$\frac{q}{m}$=20c/kg�������ǿ���������С�������ı仯�������������λ��Ч���֣���
��ͼ��ʾ���ڹ⻬��Եˮƽ�����ڽ���xoy����ϵ���ڵڢ���������ƽ�����������ǿ�糡����ǿ������x�Ḻ����ļнǦ�=45�㣬�ڵڢ�����ֱ��������������ƽ�еľ�Եƽ��C1��C2��������Ϊd1=0.6m���������ֱ���ϵ���ǿ�ų��������Ҷ���y���ϣ���C1��x���غϣ����俿����˽���������һС��M��������ԭ��O�ľ���ΪL=0.72m���ڵڢ�����ֱ��x�����һ�㹻����Եƽ��C3����һ��λ�ڴ���Q��Q����ԭ��O���d2=0.18m���ֽ�һ�������С��������ϵ�P�㣨P���ԭ��O��ͬһ�糡���ϣ����Գ��ٶ�V0=2$\sqrt{2}$m/s��ֱ�ڵ糡����������պô�ֱ��x�ᴩ��C1���ϵ�M����ų�����С�����Ϊ�ʵ㣬С��ıȺ�$\frac{q}{m}$=20c/kg�������ǿ���������С�������ı仯�������������λ��Ч���֣��� ��ͼ�����ع�ʱ���t��֪����������һ���������ë��ƻ����������ľֲ�Ƶ����Ƭ��
��ͼ�����ع�ʱ���t��֪����������һ���������ë��ƻ����������ľֲ�Ƶ����Ƭ��
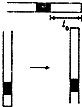 ��ͼ��ʾ�������ܵĺ����S=1cm2���ڲ���������һ������Ϊm=0.1Kg��ˮ������һ�������������壬��������ƽ��ʱ�������ij���Ϊl0=10cm���ְѲ������������ȶ����ٽ������ܵ����������ϳ�ʱ���ˮ�����ٴ��ȶ���������������������״̬��ˮ��������ڹܵ��ƶ��ľ��룬���軷���¶ȱ��ֲ��䣬����ѹǿȡP0=1��105Pa��g=10m/s2��
��ͼ��ʾ�������ܵĺ����S=1cm2���ڲ���������һ������Ϊm=0.1Kg��ˮ������һ�������������壬��������ƽ��ʱ�������ij���Ϊl0=10cm���ְѲ������������ȶ����ٽ������ܵ����������ϳ�ʱ���ˮ�����ٴ��ȶ���������������������״̬��ˮ��������ڹܵ��ƶ��ľ��룬���軷���¶ȱ��ֲ��䣬����ѹǿȡP0=1��105Pa��g=10m/s2��