题目内容
【题目】如图1所示,物体A放在足够长的木板B上,木板B静止于水平面.已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数μ1=0.2,B与水平面之间的动摩擦因数μ2=0.1,最大静摩擦力与滑动摩擦力大小视为相等,重力加速度g取10m/s2.若t=0开始,木板B受F1=16N的水平恒力作用,t=1s时F1改为F2=4N,方向不变,t=3s时撤去F2.
(1)木板B受F1=16N的水平恒力作用时,A、B的加速度aA、aB各为多少?
(2)从t=0开始,到A、B都静止,A在B上相对B滑行的时间为多少?
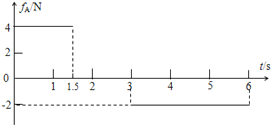
(3)请以纵坐标表示A受到B的摩擦力fA,横坐标表示运动时间t(从t=0开始,到A、B都静止),取运动方向为正方向,在图2中画出fA-t的关系图线(以图线评分,不必写出分析和计算过程).
【答案】(1)2m/s2 ;4m/s2(2)0.5s(3)fA-t的关系图线如图;
【解析】试题分析:(1)根据牛顿第二定律得对A:μ1mAg=mAaA解得:aA=μ1g=0.2×10m/s2=2m/s2
对B:F1-μ2(mA+mB)g-μ1mAg=mBaB
代入数据得aB=4m/s2
(2)t1=1s时,A、B分别为vA、vB
vA=aAt1=2×1m/s=2m/s vB=aBt1=4×1m/s=4m/s
F1改为F2=4N后,在B速度大于A速度的过程,A的加速度不变,B的加速度设为aB′,
根据牛顿第二定律得 F2-μ2(mA+mB)g-μ1mAg=mBaB′
代入数据得aB′=-2m/s2
设经过时间t2,A、B速度相等,由于AB之间的最大静摩擦力fm=μ1mAg=0.2×2.0×10N=4N
假如AB相对静止,整体分析合外力为:F合=F2-μ2(mA+mB)g=0N<fm此后它们保持相对静止.
vA+aAt2=vB+aB′t2
代入数据得t2=0.5s
A在B上相对B滑行的时间为t=t1+t2=1.5s
(3)