Question

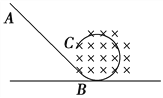
【题目】如图所示，在倾角为θ=30°的光滑斜面上放一质量为m=2kg的小球，球被竖直挡板挡住，若斜面足够长，g取10m/s2 ， 求：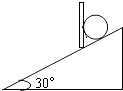

（1）球对挡板的压力N1；
（2）撤去挡板后，斜面对小球的支持力N2的大小；
（3）撤去挡板起2s末小球的速度v的大小．

Answer 1

【答案】
（1）解：以小球为研究对象，根据平衡条件，得：F1=mgtanθ=20× N= N

又由牛顿第三定律，得小球对斜面的压力大小为：N1=F1= N

答：球对挡板的压力是 N

（2）解：撤去挡板后，斜面对小球的支持力N2的大小与重力垂直于斜面方向的分力大小相等．即：N 2=mgcosθ=20× N=10 N

答：撤去挡板后，斜面对小球的支持力N2的大小是 N

（3）解：撤去挡板，重力沿斜面向下的分力提供加速度，即：

2s末小球的速度v的大小：v=at=5×2m/s=10m/s

答：撤去挡板起2s末小球的速度v的大小是10m/s

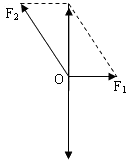
【解析】小球处于静止状态，受到重力G、木板的弹力F1和斜面的支持力F2，根据平衡求出弹力和支持力．再由牛顿第三定律求出小球对斜面的压力和球对挡板的压力．
【考点精析】认真审题，首先需要了解牛顿第三定律(牛顿第三运动定律指出了两物体之间的作用是相互的，因而力总是成对出现的，它们总是同时产生，同时消失；作用力和反作用力总是同种性质的力；作用力和反作用力分别作用在两个不同的物体上，各产生其效果，不可叠加)．