题目内容
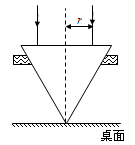
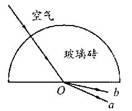
(9分)在桌面上有一倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示。有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为1.5,求光束在桌面上形成光斑的面积。

4πr2
试题分析:如图所示,设玻璃圆锥与桌面的交点为A,右侧边缘的光束垂直射入圆锥后交三角形于O点,入射角为α,则有
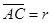 ,
, 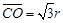 ,α=60°,有
,α=60°,有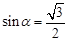 (2分)
(2分)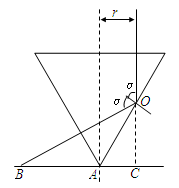
对临界角C有:
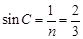 ,
,比较得α>C,所以在O点发生了全反射。光线从左面射出。(3分)
由图中几何关系得,光射到左面时垂直射出,不折射,射到桌面在B点, 有
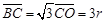 ,则
,则 (2分)
(2分)从轴线向右侧的入射线,最后射到桌面上AB之间,这样光束在桌面上形成的光斑是以A为圆心,AB为半径的圆,得光斑面积S=π(2r)2=4πr2。(2分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

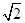 。人工打磨成球形后置于空气中(如图所示),已知球半径R=10 cm,MN是一条通过球心O的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为d=5
。人工打磨成球形后置于空气中(如图所示),已知球半径R=10 cm,MN是一条通过球心O的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为d=5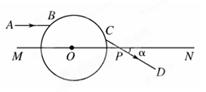
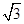 ,AB是一条直径,今有一束平行光沿AB方向射向圆柱体. 若一条入射光经折射后恰经过B点,试求:
,AB是一条直径,今有一束平行光沿AB方向射向圆柱体. 若一条入射光经折射后恰经过B点,试求: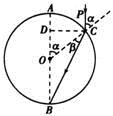
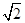
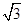
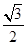
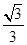
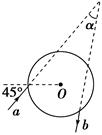
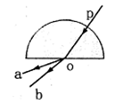
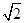 的透明球表面,入射角为45°,在球的内壁经过一次反射后,从球面射出的光线为b,则入射光线a与出射光线b之间的夹角α为( )
的透明球表面,入射角为45°,在球的内壁经过一次反射后,从球面射出的光线为b,则入射光线a与出射光线b之间的夹角α为( )