题目内容
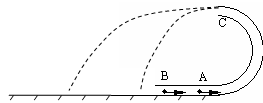
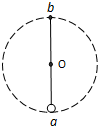
质量相同的两个小球，分别用长度相同的细杆和细绳悬于各自的固定点要使它们绕固定点在竖直平面里做圆周运动，这两个小球通过最低点时的最小速度之比等于
| A．1：1 | B．1：2 | C．2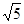： | D．3： |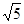
C
轻杆带着物体做圆周运动，只要物体能够到达最高点就可以了，所以速度可以为零，故在最高点的最小速度为零；
若把轻质细杆改成细绳，小球在最高点绳子的拉力与重力的合力提供向心力，当绳子的拉力为零时，刚好做圆周运动，速度最小，则有；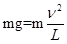
,
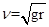
小球从最低点A点运动到最高点B点，根据机械能守恒定律有：
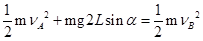，解得两个小球通过最低点时的最小速度之比等于2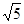：：要了解物体做圆周运动的特点，同时也用到机械能守恒，是一个很好的综合题目，很能考查学生的分析解题能力．
若把轻质细杆改成细绳，小球在最高点绳子的拉力与重力的合力提供向心力，当绳子的拉力为零时，刚好做圆周运动，速度最小，则有；
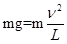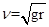
,小球从最低点A点运动到最高点B点，根据机械能守恒定律有：
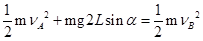，解得两个小球通过最低点时的最小速度之比等于2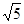：：要了解物体做圆周运动的特点，同时也用到机械能守恒，是一个很好的综合题目，很能考查学生的分析解题能力．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
